Hexágono con dos vértices apoyados en dos rectas y un lado apoyado en una tercera recta PAU Valencia – 971
Inicio > Geometría plana > Homotecia y semejanza
Dibuje un hexágono regular ABCDEF de forma que tenga el vértice A sobre la recta r, el B sobre la recta r’ y el lado CD sobre la recta s. (PAU Valencia 2013)
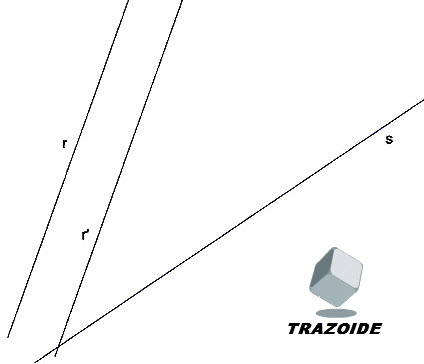
SOLUCIÓN
OPCIÓN I (Traslación y homotecia)
1 – Dibujar un hexágono cualquiera A»B»C»D»E»F» que tenga uno de sus lados C»D» apoyado en la recta s.
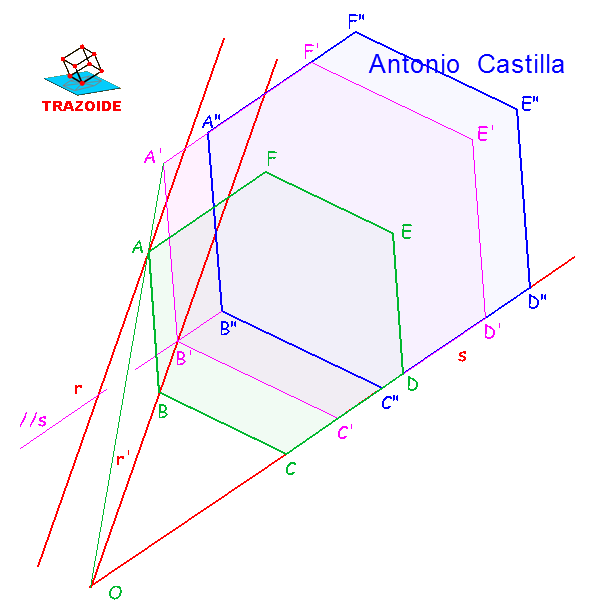
2 – Por el vértice B» trazar una paralela a la recta s (traslación) hasta cortar a la recta r’. Esto nos da vértice B’ de un nuevo hexágono, A’B’C’D’E’F’, igual al anterior pero que ya tiene un vértice sobre r’ y un lado en s.
3 – Unir el vértice A’ con el punto de corte de las rectas r’ y s (este es el centro O de una homotecia). Donde corte a la recta r’ es el vértice A del hexágono buscado, ABCDEF.
4 – A partir de A y mediante paralelas a los hexágonos anteriores dibujar el hexágono pedido.
OPCIÓN II (Homotecia)
5 – Tomar un punto cualquiera, D», sobre la recta Dibujar un hexágono cualquiera A»B»C»D»E»F» que tenga uno de sus lados C»D» apoyado en la recta s.
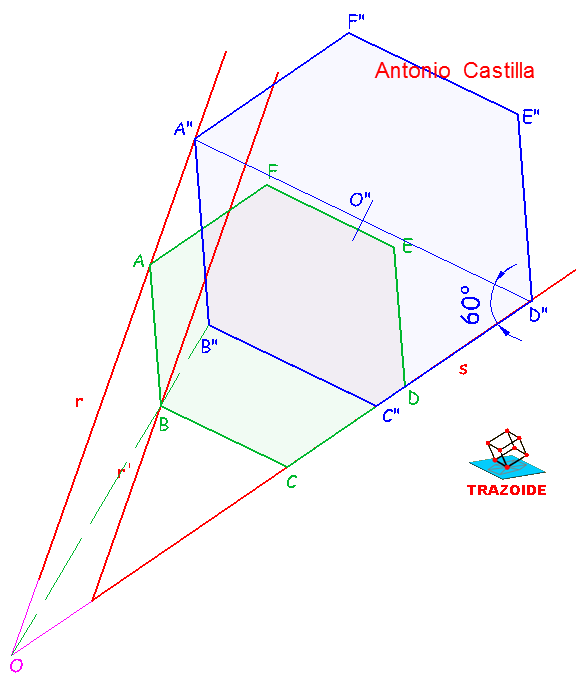
6 – Desde ese punto levantar una línea (diagonal de un hexágono) que forme 60º con la recta s. El punto de corte con la recta r es el vértice opuesto, A», del hexágono.
7 – Conocida la diagonal, A»-D», del haxágono dibujarlo.
8 – Unir el punto de corte de las rectas r y s, O (centro de homotecia), con el vértice B», donde corte a la recta r’ es el vértice B del hexágono buscado.
9 – A partir de B y mediante paralelas a los hexágonos anteriores dibujar el hexágono pedido.
OPCIÓN III (Homotecia)
9 – Dibujar un hexágono cualquiera A»B»C»D»E»F» que tenga uno de sus lados C»D» apoyado en la recta s.
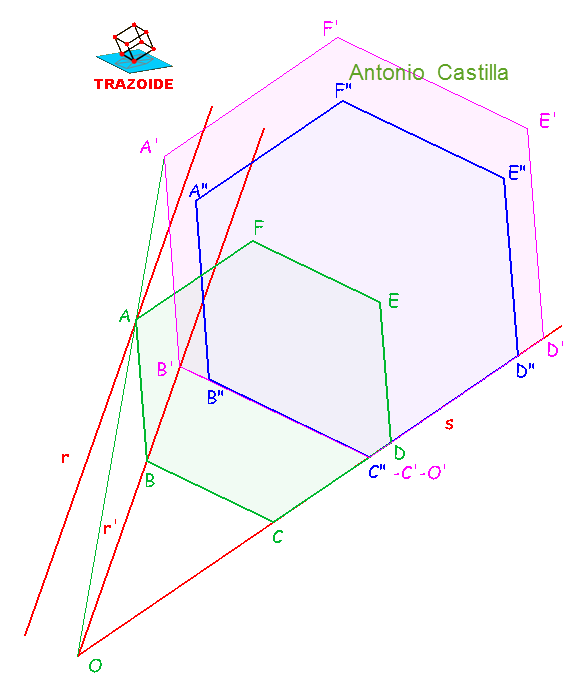
10 – Utilizar el vértice C» como centro de homotecia, O», y uniendo O» con B» se obtiene B’ en r’. Esto nos da vértice B’ de un nuevo hexágono, A’B’C’D’E’F’, que ya tiene un vértice sobre r’ y un lado en s.
11 – Unir el vértice A’ con el punto de corte de las rectas r’ y s (este es el centro O de otra homotecia). Donde corte a la recta r’ es el vértice A del hexágono buscado, ABCDEF.
12 – A partir de A y mediante paralelas a los hexágonos anteriores dibujar el hexágono pedido.
Inicio > Geometría plana > Homotecia y semejanza | | Vídeos sobre homotecia | | Vídeos sobre semejanza





