Inicio > Sistema acotado > Cubiertas
Determinar los ejes principales de la elipse que forma la intersección entre una cubierta cónica y una plana.
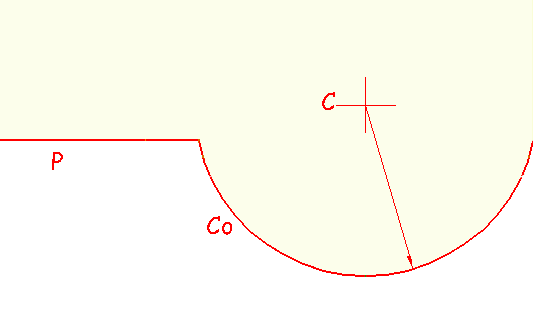
El plano tiene línea de alero (o cota cero) en la recta P (en rojo), y la cubierta cónica es de alero Co y centro C.
SOLUCIÓN
1 – Levantamos una línea (en verde, marcada con la palabra «Perfil») perpendicular a las líneas de cota del plano.
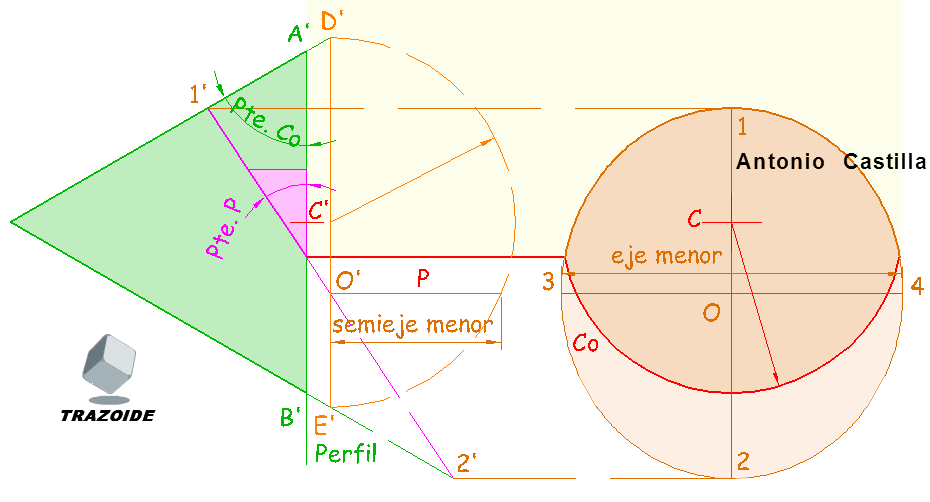
2 – Donde la línea de cota cero del plano toca al perfil se construye el triángulo de la pendiente (el triángulo en magenta, acotado con las siglas «Pte. P»). Recuerda que el denominador de la pendiente se coloca sobre la línea del perfil mientras que el numerador en perpendicular a ella.
3 – Se lleva el centro, C, del cono hasta la línea del perfil, C’. Desde el centro C’ y con el mismo radio del cono se dibujan los extremos de la base del cono, A’ y B’. Por estos se dibuja la pendiente del cono (acotada como «Pte. Co»). El triángulo formado (en verde) es el perfil del cono.
4 – Prolongamos la hipotenusa del triángulo de la pendiente del plano en los dos sentidos hasta tocar al cono en los puntos 1′ y 2′.
5 – Se dibujan paralelas a las líneas de cota del plano por esos puntos, 1′ y 2′, hasta la perpendicular a las líneas de cota del plano que pasa por el centro C del cono. Los puntos obtenidos, 1 y 2, dan el eje mayor de la elipse buscada (la intersección del plano y el cono).
6 – El punto medio entre los extremos del eje mayor, 1-2, es el centro, O, de la elipse. También se puede hallar en el perfil como punto medio entre 1′-2′, dando O’, y después llevarlo a la proyección horizontal.
7 – En el perfil, por el centro de la elipse O’ se traza una paralela a la base del cono hasta tocar a sus contornos, D’ y E’. Con centro en el punto medio de D’-E’ se traza una semicircunferencia (o una completa). Desde el centro O’ dibujamos una perpendicular a la base del cono y la medida que hay entre el centro O’ y la semicircunferencia es el semieje menor.
8 – En la proyección horizontal, por el centro de la elipse, O, dibujamos una paralela a las líneas de cota del plano y sobre ella llevamos la medida del eje menor, obteniendo los puntos 3 y 4 que forman el eje menor de la elipse.
9 – Conocidos el eje mayor, 1-2, y el eje menor, 3-4, puedes obtener cualquier otra magnitud de la elipse o el trazado de los puntos que la forman.
El perfil se puede tomar sobre el diámetro del cono perpendicular a las líneas de cota del plano, pero eso crea más confusión al tener la proyección horizontal y el perfil uno encima del otro, por eso yo prefiero hacerlo aparte.
Recuerdo, también, que dependiendo de la pendiente del plano y del cono podría dar una de las otras dos curvas cónicas (hipérbola o parábola).
Inicio > Sistema acotado > Cubiertas
Cubierta – 984





