Ejercicios de PIRÁMIDES en diédrico resueltos – 997
Inicio > Sistema diédrico > Pirámides
Sobre un plano "alfa"(-30, 30, 30) se apoya una pirámide recta de 60 mm de altura; se sabe que los vértices de la base son los puntos A(0, 20, Z) B(40, 0, Z) C(20, 35, Z).
Hallar:
a) Las proyecciones diédricas de la pirámide.
b) La longitud real de las aristas AB y CV, siendo V el vértice opuesto de la base.
SOLUCIÓN
1 – Sitúa el plano.
2 – Sitúa los puntos A, B y C. Para el punto B, la proyección vertical del punto la tienes sobre la traza vertical del plano por tener alejamiento cero. Para los puntos A y C utiliza una recta horizontal o frontal para localizar su otra proyección.
3 – Localiza el baricentro del triángulo ABC en ambas proyecciones.
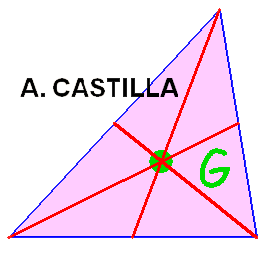
4 – Por los baricentros levanta rectas perpendiculares a las trazas del plano.
En el siguiente dibujo lo aclaro.
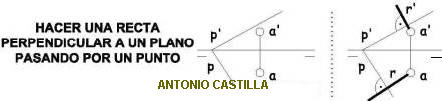
5 – Sobre esa perpendicular y a partir del baricentro tienes que hallar la proyección de la altura de la pirámide, 60 mm. Este es el vértice V.
En el siguiente dibujo pongo los pasos a seguir
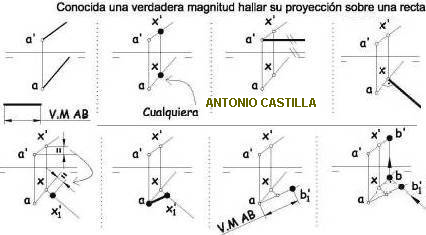
6 – Une el vértice V con ABC. Ya tienes la pirámide.
7 – Determinas las distancias que hay entre AB y CV.
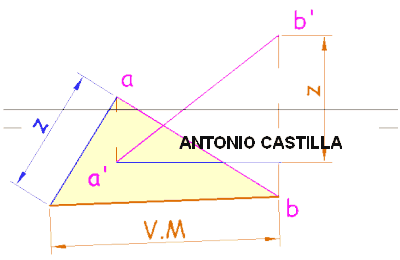
Inicio > Sistema diédrico > Pirámides | |





