Inicio > Sistema diédrico > Pirámides
Pirámide conocidos dos puntos de la base y el vértice.
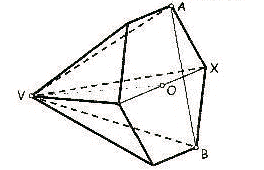
Se ha considerado una pirámide recta de base hexagonal (ver perspectiva adjunta) para la elaboración de patas niveladoras de máquinas. Se pide :
1.- Representar las proyecciones de la entrecara y determinar su magnitud.
2.- Representar el plano determinado por A, B y V.
3.- Representar las proyecciones del centro de la base y determinar la altura de la pirámide.
4.- Representar las proyecciones de la pirámide.
5.- Representar el plano beta determinado por B, X y el punto medio de la altura.
6.- Representar las proyecciones y VM de la sección que origina beta sobre el sólido.
DATOS :
A ( Alejamiento = 11 mm; Cota = – 31 mm; Distancia al margen derecho del formato = 72 mm)
B ( Alejamiento = 67 mm; Cota = 23 mm; Distancia al margen derecho del formato = 78 mm)
C ( Alejamiento = – 36 mm; Cota = 64 mm; Distancia al margen derecho del formato = 159 mm)
El único vértice de la base que se encuentra a dereha de A y B es X.
NOTA : Este ejercicio se resolverá en un formato A4 en posición vertical, representándose la L.T. en horizontal y dividiendo al formato en dos superficies iguales.
SOLUCIÓN
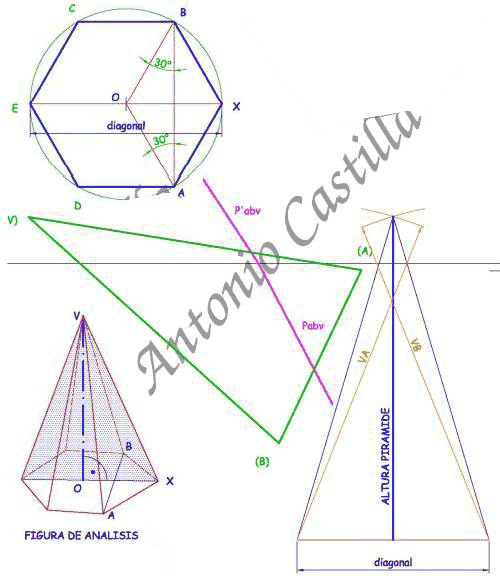
Para la determinación de las magnitudes de la pirámide se construirá un hexágono con el valor entre caras de la magnitud AB abatida. Para ello basta con levantar dos líneas a 30º y donde se corten es el centro del hexágono.
De dicho hexágono se determina el valor de su diagonal, la cual se utilizará para dibujar la sección media de la pirámide (ver la figura de análisis), que es un triángulo isósceles de lados iguales a la magnitud VA y VB tomadas del abatimiento.
La altura de la sección media es el valor de la altura de la pirámide.
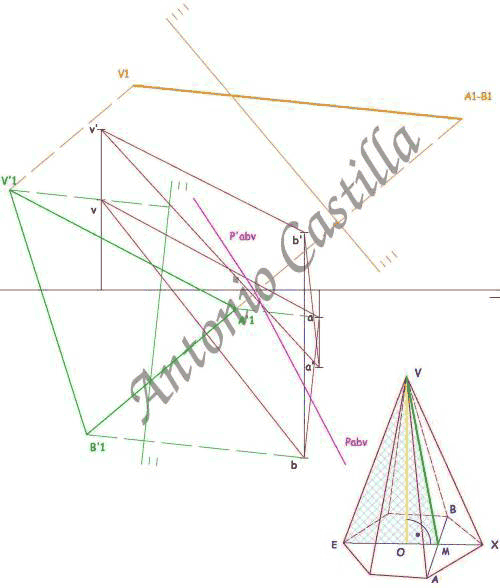
Si la recta AB fuese vertical (o de punta), la sección ABV sería proyectante a la vez que la base hexagonal también (ver la figura de análisis).
En esa situación la sección VME estará en verdadera magnitud, la cual está formada por cantidades ya averiguadas anteriormente. Si se prefiere se puede trabajar con la sección VOM.
Para ello se debe colocar la recta AB en posición vertical (o de punta), para lo que se recurre a dos cambios de plano. El primer cambio de plano (en verde) con la línea de tierra paralela a la proyección horizontal de AB y la tercera perpendicular (en naranja).
En el último cambio de plano se dibujará la sección VAE (en azul oscuro) en verdadera magnitud, siendo VE el valor de la arista lateral del cono deducida anteriormente y el segmento ME extraído del hexágono que se dibujó en verdadera magnitud anteriormente.
Si por el vértice V1 se hace una perpendicular (en amarillo) al lado A1-E1 se obtiene la altura y el centro de la base, O1.
También se podría haber trabajado con el triángulo VMO y de esa manera obtener directamente la posición del centro.
Se deshace el cambio de plano (líneas azul claro y naranja) del centro, O, de la base. Siendo el plano VEO proyectante en la otra proyección, por lo que el centro O estará sobre la altura del triángulo VAB.
Para las otras proyecciones se lleva la medida correspondiente (s y t).
Las proyecciones del punto E se determinan de la misma forma (en marrón y naranja) que las del centro O (medidas u y v).
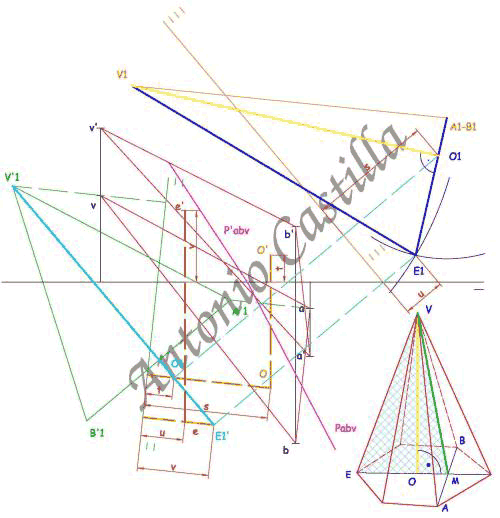
Como el hexágono es simétrico y ya se conocen tres vértices, A-B-E, y el centro, O, basta con unir las proyecciones de esos puntos con el centro y llevar esa misma distancia hacia el otro lado (ver la figura de análisis de la parte superior).
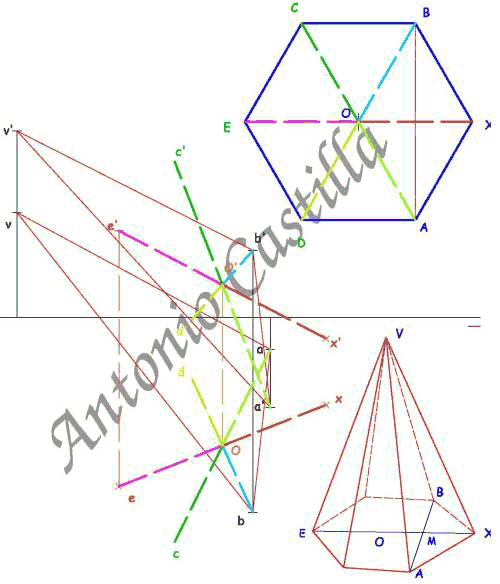
Ya solo queda unir los seis vértices de la base entre sí y con el vértice de la pirámide.
Inicio > Sistema diédrico > Pirámides | |





