Ejercicios resueltos en el sistema acotado – 995
Inicio > Sistema acotado > Ejercicios en sistema acotado
El punto O (120, 150, 40) es el centro de una esfera de 40 mm de radio. Dicha esfera es seccionada por el plano P cuya traza pasa por A (120, 150, 0) y es paralela al lado más largo del papel formando 45º con el plano de proyección y ascendiendo de derecha a izquierda.
Por el punto B (120, 150, 80) se hace pasar otro plano Q de traza paralela a la de P que forma 22,5º con el plano de proyección ascendiendo también de derecha a izquierda.
Se pide hallar la proyección del cono secante a la esfera que corta a esta según las secciones producidas por P y Q y dibujar las proyecciones de esta y la traza del cono.
SOLUCIÓN
1 – Colocar el centro O y dibujar la esfera (en negro rellena de gris).
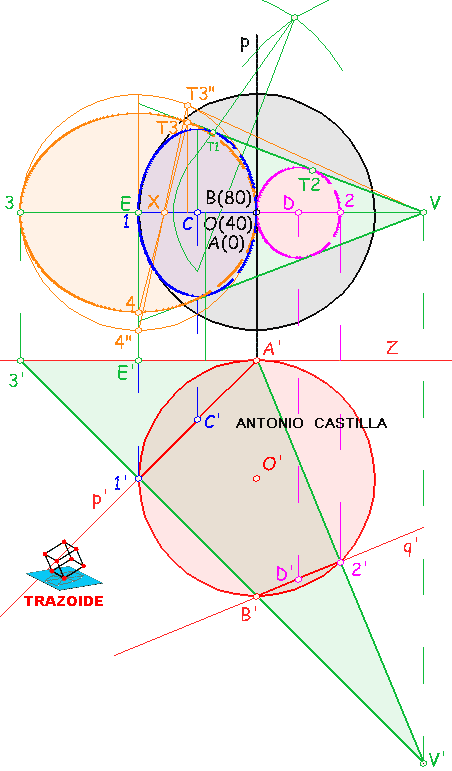
2 – Colocar el punto A y dibujar la traza del plano P, una vertical que pasa por A (en negro).
3 – Colocar el punto B, que coincide en proyección con O y A, aunque a distinta cota.
4 – Dibujar una línea, Z, perpendicular a la traza P que nos servirá para levantar un perfil (alzado).
5 – Llevar los punto O, A y B al perfil, O’, A’ y B’. Con centro en O’ y el radio de la esfera se dibuja esta. Por el punto A’ y a 45º se traza el plano p’, y por B’ y a 22,5º se levanta el plano q’.
6 – Donde corte a la esfera, A’-1′ y B’-2, son las secciones (circunferencias) de los planos P y Q sobre la esfera.
7 – Sobre una perpendicular a la traza P se llevan las proyecciones de 1 y 2 (de A y B ya se tiene). Estas nos dan los ejes menores, A-1 y B-2, de las elipses en las que quedan proyectadas las circunferencias.
8 – Por el punto medio, C y D, de los ejes menores, A-1 y B-2, y perpendicular a ellos se llevan los ejes mayores que son iguales a las medidas de A’-1′ y B’-2′ tomadas del perfil.
9 – Conocidos los ejes de las elipses dibujarlas (en azul y magenta).
10 – En el perfil se unen los puntos 1′ con B’ y A’ con 2′. Estas dos líneas son el contorno del cono en el perfil. Donde se cortan, V’, es su vértice.

11 – Llevar el perfil del vértice, V’, a la línea 1-2 obteniendo su proyección, V.
12 – Desde V se dibujan las tangentes a las elipses (en verde). Estos son los contornos aparentes del cono, y sus puntos de tangencia T1 y T2.
13 – En el perfil prolongar el cono hasta cortar a Z (punto A’ y 3′). Esta es la medida del eje mayor de la elipse intersección (traza) del cono con el plano horizontal.
14 – Llevar los puntos A’ y 3′ hasta la línea V-1 para conseguir sus proyecciones 3 y A (que ya teníamos).
15 – Su punto medio, E, es el centro de la elipse. Con centro en E y radio E-A se dibuja una circunferencia (afín de la elipse), en naranja.
16 – Desde V se traza la tangente a la circunferencia. Su punto de tangencia es T3".
17 – Desde T3" bajar una perpendicular a V-A y donde corte al contorno del cono, V-T1, es el punto de tangencia, T3, de la elipse con el contorno del cono.
18 – Unir T3" con el punto, 4", de corte de la perpendicular a V-A por E.
19 – Donde corte a V-A (eje de afinidad, punto X) se une con T4. Donde esta última corte a E-4" es el extremo, 4, del eje menor de la elipse.
20 – Conocidos los semiejes 3-E y 4-E se dibuja la elipse.
Inicio > Sistema acotado > Ejercicios en sistema acotado | |





