Tetraedro con altura y el ortocentro en diédrico – 983
Inicio > Sistema diédrico > Tetraedros
Los puntos M y N definen una recta r, se pide :
– Las trazas el plano paralelo a la L.T. y que contenga a la recta dada.
– Las proyecciones de un tetraedro de altura 45 mm, con una cara contenida en el plano dado y con ortocentro en el punto H (45, y, 15). Se sabe que la altura de esa cara forma 30º con el plano horizontal de proyección, con el vértice de esta, de mayor cota y a la derecha.
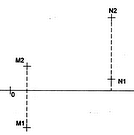
SOLUCIÓN
Un problema un poco largo y completo. Como está formado por varias partes distintas las explicaré en varias partes.
Hallar un plano paralelo a la línea de tierra que contenga a dos puntos, M y N
1 – Unir los dos puntos, M y N, formando una recta.
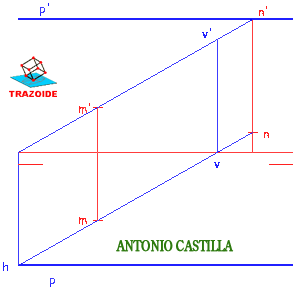
2 – Hallar las trazas de la recta, H y V.
3 – Por la traza horizontal, h, se dibuja una paralela a la línea de tierra y esa es la traza horizontal del plano, p.
4 – Por la proyección vertical se traza otra paralela a la línea de tierra y esa es la traza vertical del plano, p’.
5 – Si se desea el perfil del plano, llevar los puntos M y N al perfil y unirlos entre sí.
Por una cuestión de comodidad mía, al punto H(45, y,15), yo le he llamado O.
Dada la proyección vertical de un punto, O(45, y, 15), contenido en un plano, P, paralelo a la línea de tierra hallar su proyección horizontal
6 – PRIMER PROCEDIMIENTO : dibujar una recta cualquiera que pase por la proyección vertical, O’
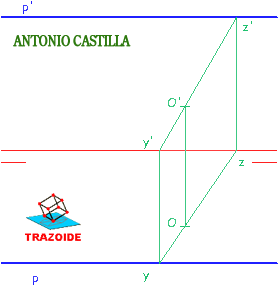
7 – Donde corte a la línea de tierra, y’, se baja hasta la traza horizontal del plano, y.
8 – Donde corte a la traza vertical del plano, z’, se baja hasta la línea de tierra.
9 – Uniendo esos puntos, z e y, se obtiene una recta en la que estará el punto.
10 – Bajar una perpendicular a la línea de tierra hasta y-z y esa es la proyección horizontal del punto, O.
11 – SEGUNDO PROCEDIMIENTO : Llevar la proyección vertical del punto, O’, hasta el perfil del plano mediante una paralela a la línea de tierra (Puedes verlo pulsando aquí).
12 – Deshacer el perfil para determinar la proyección horizontal del punto, O.
Hallar una recta contenida en un plano paralelo a la línea de tierra y que pasa por el punto O (de ese plano) y forma 30º con el plano horizontal de proyección
13 – Desde la proyección vertical del punto, O’, se trazan líneas que formen con la línea de tierra el ángulo dado con el plano horizontal de proyección, 30º.
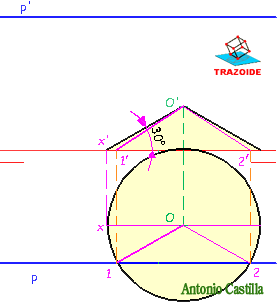
14 – Donde corte a la línea de tierra, punto x’ (da igual que sea a la derecha o a la izquierda) se baja hasta una paralela a la línea de tierra que pasa por O, dando x.
15 – Con centro en O y radio hasta x se traza una circunferencia.
16 – Donde la circunferencia corte a la traza horizontal del plano, puntos 1 y 2, se unen con el punto O, y esas son las dos posibles soluciones.
17 – Subir los puntos 1 y 2 hasta la línea de tierra, 1′ y 2′, y unir con O’ para determinar sus proyecciones verticales.
18 – De las dos posibles soluciones, O-1 y O-2, se elegirá O-1 por que a medida que los puntos van hacia la derecha aumentan de cota, como pide el enunciado.
Determinación de las magnitudes de un tetraedro regular conocida la altura del cuerpo, 45 mm
19 – Dibujar un triángulo equilátero de lado cualquiera, L’ (el de la izquierda).
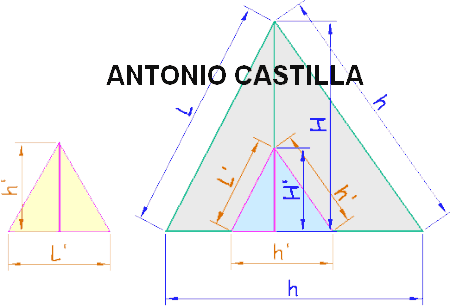
20 – Determinas la altura de ese triángulo, h’.
21 – Construir un triángulo isósceles (el más pequeño de la derecha) con las medidas L’, h’ y h’.
22 – Se dibuja la altura, H’.
23 – Sobre H’ se coloca el valor conocido de la altura del tetraedro, H = 45 mm, que nos dan.
24 – Por su extremo se trazan dos paralelas a los lados del triángulo.
25 – Los lados de este nuevo triángulo están formados por los valores buscados del lado del tetraedro, L, y de la altura de cara, h.
Triángulo equilátero contenido en un plano paralelo a la línea de tierra, del que se conoce su ortocentro O y la recta sobre la que se apoya una de sus alturas O-1 y el valor de dicha altura
26 – Se abate el ortocentro O. Para ello hay dos procedimientos, utilizando el perfil (pulsar aquí para recordarlo) o sin utilizar el perfil (pulsar aquí).
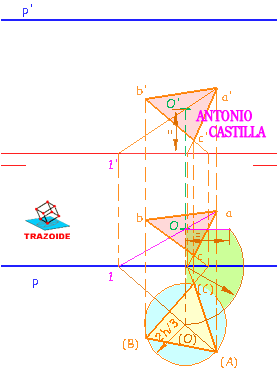
27 – El punto 1 ya esta abatido por encontrase sobre el plano horizontal de proyección. Uniendo (1) con (O) se tiene la recta en la que se apoya la altura del triángulo.
28 – En un triángulo equilátero el baricentro, el ortocentro, el incentro y el circuncentro son todos coincidentes, y lo mismo las medianas, las alturas, las bisectrices y las mediatrices. Por lo tanto, desde el ortocentro hasta cualquiera de los tres vértices hay una longitud igual a 2/3 de la altura del triángulo, h.
Con centro en (O) y 2h/3 se traza una circunferencia, donde esta corte a la altura del triángulo, (1)-(O), es el primer vértice del triángulo, (A).
29 – Con centro en (A) y radio el lado del triángulo, L, se traza un arco que cortará a la circunferencia anterior en dos puntos, (B) y (C), los restantes vértices del triángulo buscado.
30 – Desabatir los puntos obtenidos, (A)-(B)-(C), mediante el perfil (proceso inverso al realizado, pulsar aquí) o bien mediante afinidad (pulsar aquí para verlo).
31 – Hallar la proyección vertical de los puntos mediante el perfil (primer método, pulsar aquí) o apoyándose en una recta (segundo método, pulsar aquí).
Tetraedro con una cara apoyada en un plano paralelo a la línea de tierra
32 – Desde su baricentro O (que coincide en este caso con el ortocentro), se levanta sendas perpendiculares a las trazas del plano, P.
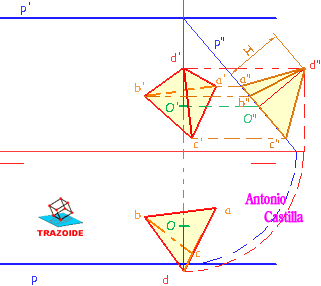
33 – Se lleva el punto O al perfil, O", sobre el plano, p", y a partir de él se levanta una perpendicular al plano.
34 – En esa perpendicular se mide en verdadera magnitud el valor de la altura del cuerpo, H, dando el cuarto vértice, d".
35 – Llevar ese punto D a las otras proyecciones sobre las perpendiculares a las trazas del plano, proyecciones d y d’.
36 – Unir el punto D con los puntos de la base, A-B-C.
37 – Determinar la visibilidad de las aristas.
Inicio > Sistema diédrico > Tetraedros | | Vídeos sobre tetraedros





