Determinación del baricentro, circuncentro, incentro y ortocentro – Ejercicios de TRIÁNGULOS – 899
Inicio > Geometría plana > Triángulos
Determinación del baricentro, circuncentro, incentro y ortocentro.
SOLUCIÓN
La forma de obtener los puntos notables de un triángulo es la siguiente :
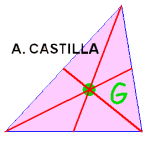
BARICENTRO de un triángulo
Es el centro de gravedad de un triángulo. Se obtiene como intersección de las medianas (líneas que unen los vértices con los puntos medios de los lados opuestos).
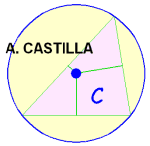
CIRCUNCENTRO de un triángulo
Es el centro de la circunferencia circunscrita. Se obtiene como intersección de las mediatrices (perpendiculares a los lados por los puntos medios).
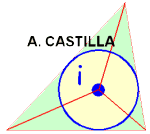
INCENTRO de un triángulo
Es el centro de la circunferencia inscrita. Se obtiene como intersección de las bisectrices (líneas que dividen los ángulos en dos partes iguales).
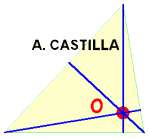
ORTOCENTRO de un triángulo
Se obtiene como intersección de las alturas (rectas perpendiculares a los lados y que pasan por los vértices opuestos).
Inicio > Geometría plana > Triángulos | | Vídeos sobre triángulos





