Inicio > Geometría plana > Triángulos
Triángulo dada la bisectriz, la mediana y la altura de un mismo ángulo.
SOLUCIÓN
Se construye un triángulo rectángulo A E D, tomando por cateto A E la altura h, y por hipotenusa A D la mediana ma, trazando por D una perpendicular al cateto base E D. Con centro en el vértice A y radio wa, bisectriz conocida, se describe un arco hasta cortar en F al cateto básico E D, prolongando el segmento A F hasta cortar en G a la perpendicular trazada anteriormente por D.
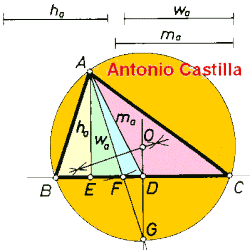
La mediatriz del segmento A G corta a la perpendicular ya indicada en el punto O, punto que se toma como centro para trazar una circunferencia auxiliar que pase por A y G. Esta circunferencia corta a las prolongaciones de E D en los puntos B y C, vértices del triángulo solución ABC.
Inicio > Geometría plana > Triángulos | | Vídeos sobre triángulos





