TRAZOIDE

Hallar el centro de inversión que transforma tres puntos dados no alineados en los vértices de un triángulo equilátero.

En el ejercicio https://trazoide.com/inversion_999/ se explica el inverso de un triangulo y se obtiene un triangulo curvilineo,



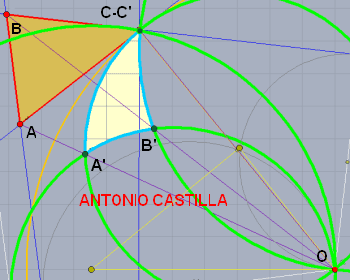
y en el https://trazoide.com/inversion_991/ interpreto que se trata de que los vértices de este triangulo curvilíneo sean equidistantes.

Me pregunto si independientemente de cuales sean los puntos de partida siempre sus inversos serán equidistantes???

.
El problema está mal resuelto, porque según dice el enunciado partimos de tres puntos no alineados y debemos buscar el triángulo equilátero, mientras que la solución se ha planteado al revés, con el triángulo equilátero se han buscado los tres puntos.

Es un problema que se publicó hace mucho tiempo, y seguramente durante los cambios que hice de un servidor a otro y de un lenguaje a otro, acabé mezclando dos problemas parecidos pero distintos.

A ver si encuentro un ratillo y lo modifico.

Por echar una manilla a Antonio hasta que prepare su dibujo, adelantaré que las intersecciones de las circunferencias de Apolonio respecto del triángulo dado son los centros de inversión positiva o negativa .El valor de +- r(K) puede ser el que queramos, por tanto habrá infinitas soluciones pero por lo general partirán de 2 básicas (2 intersecciones) y las demás semejantes. Los triángulos de puntos equiláteros serán curvilíneos si se transforman los lados.
Saludos.

.
El que quiera puede aportar, porque ahora ni siquiera tengo Autocad, por un fallo he tenido que desinstalarlo, así que tardaré en contestar.

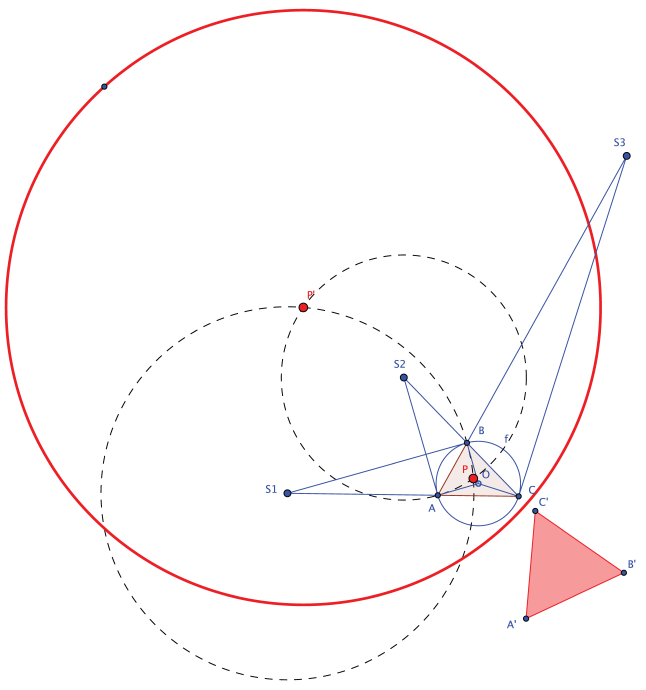
La solución, como avanzaba Fleitas, hace uso de las circunferencias de Apolonio. INVERSIÓN DE CUALQUIER TRIÁNGULO EN UNO EQUILÁTERO.

1. Sea ABC el triángulodado y f su circuncírculo, de centro O.
2. Trazar las tangente a f por A, B y C.
3. Producir las intersecciones S1, S2 y S3 de esas tangentes con las prolongaciones de los lados opuestos.
4. Las intersecciones estarán alineadas (Recta de Lemoine, en azul).
5. Trazar las 3 circunferencias de Apolonio (trazo discontinuo), con centros en S1, S2 y 53 y radios hasta el vértice de que procede cada tangente.
Las 3 circunferencias confluyen en los puntos rojos: P y P'.
6. Con centro en P o en P' (como en el dibujo) y cualquier radio trazar la circunferencia de inversión (roja) de A, B y C, obteniéndose el triángulo equilátero A'B'C' buscado (en rojo).

Hola.
El año pasado realicé una animación de éste problema pero no llegué a publicarlo en el foro.
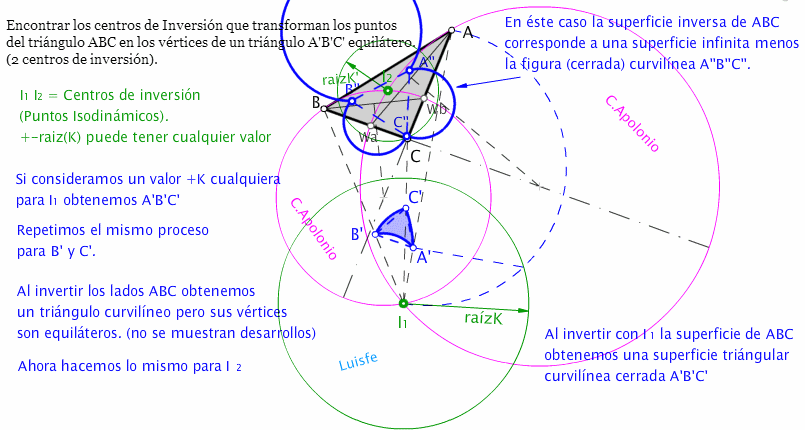
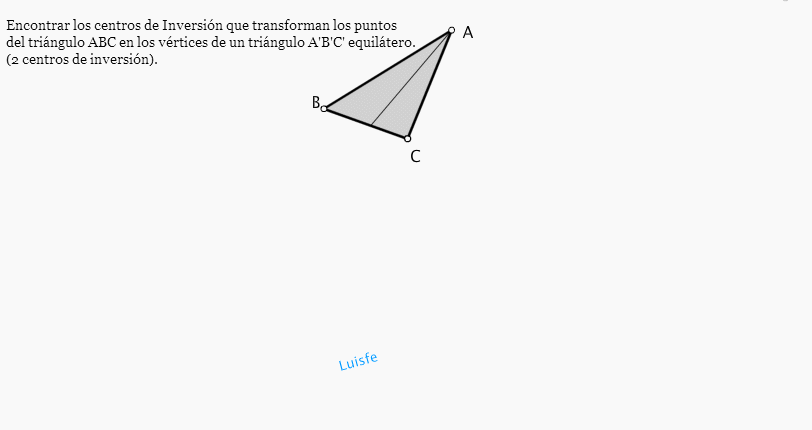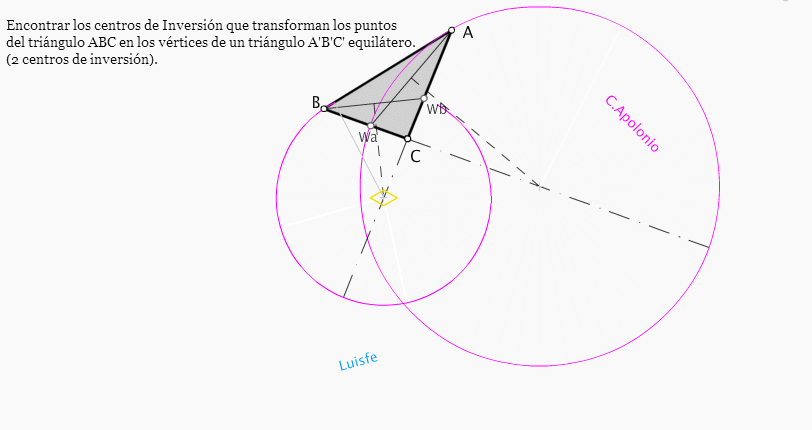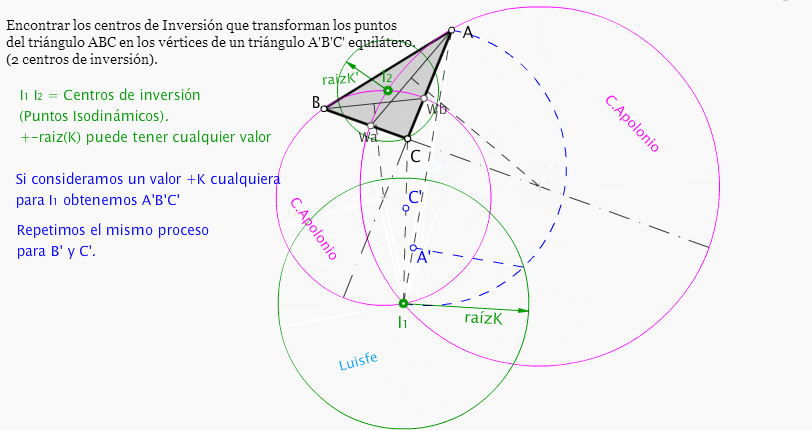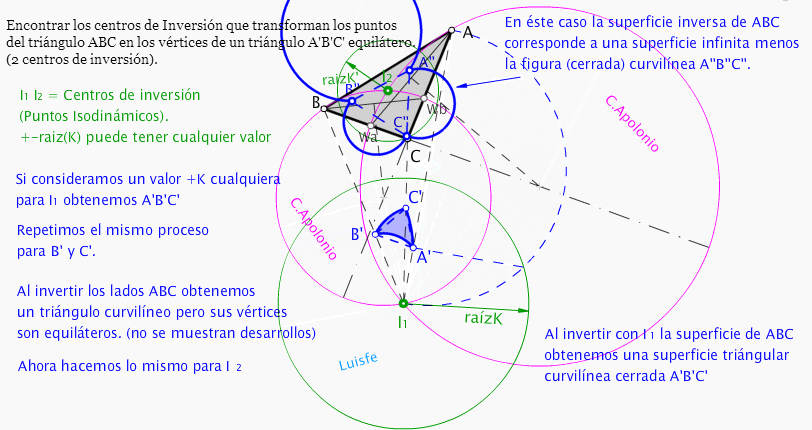
La forma que muestro para hallar las circunferencias de Apolonio difiere de la descrita por A.Briones (que es perfecta) , pero creo que no es lo realmente importante en éste ejercicio. Relevante es acordarse de que las
intersecciones de dichas circunferencias son los centros de Inversión buscados. Luego procedemos a dar un
valor cualquiera para r(K) (inversión positiva o negativa).
Por si es de interés, ahí va:

Saludos.

Imágenes alternativas :

Antonio Castilla escribió:... El problema con las conversiones venía de que tú imagen era enorme ...

Gracias por la explicación y disculpa. Soy muy mal informático, he de reconocerlo.

Hola a tod@s
Ahí va mi aporte a este problema que, básicamente, es el de Luisfe pero si aporta algo, pues mira qué bien.

Necesitamos conocer:
1. El lugar geométrico de los puntos P cuya razón de distancias a dos puntos fijos A, B es una constante k ≠ 1 es una circunferencia que se llama circunferencia de Apolonio. Este teorema se demuestra a partir del teorema de las bisectrices de un triángulo.
2. Dado un triángulo ABC la circunferencia de Apolonio de un lado, por ejemplo el AC, es una circunferencia de diámetro los puntos donde las bisectrices (interior y exterior) del tercer vértice B cortan al lado AC o a su prolongación.
3. Las tres circunferencias de Apolonio de un triángulo se cortan en dos puntos especiales que se llaman puntos isogonales y que tienen la propiedad de ser inversos en la inversión cuya circunferencia de puntos dobles es la circunferencia circunscrita al triángulo.
4. La inversión de centro uno de los puntos isogonales y circunferencia de puntos dobles cualquiera nos da como inversos de ABC los vértices de un triángulo equilátero.

PROCEDIMIENTO

Con los tres puntos no alineados formamos un triángulo ABC
Sobre dos de sus lados se levanta la circunferencia de Apolonio. Esas circunferecias se cortan en dos puntos que serán los puntos isodinámicos que buscamos
Para ello consideramos el lado AC y desde B trazamos sus bisectrices que cortan a la recta AC en los puntos M, N.
Trazamos la circunferencia c1 de diámetro MN.
Lo mismo para el lado BC y tenemos la circunferencia c2 de diámetro M1N1
Las dos circunferencias se cortan en dos puntos llamados puntos isodinámicos P1, P2
Tomando uno de los puntos isodinámicos P1 como centro de inversión y círculo de inversión (cpd) cualquiera tenemos que A'B'C' que son los inversos de ABC determinan un triángulo equilátero
Los mismo si tomamos P2 como centro de inversión y radio de inversión cualquiera.
Un saludo