Página 1 de 1
circunferencias tangentes a otra, una recta y punto
Publicado: Vie, 10 Oct 2008, 07:38
por Ruizmt
¡¡¡Hola!!!
Quisiera resolver el caso de
circunferencias tangentes a una circunferencia, a una recta que corta a esa circunferencia y a un punto (el punto dentro de la circunferencia).
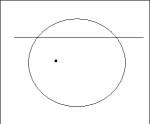
Muchas gracias de antemano.
Un saludo.
Publicado: Vie, 10 Oct 2008, 08:00
por Antonio Castilla
.
1 - Hacer una perpendicular a la recta por el centro de la circunferencia; donde corte a la circunferencia son los puntos A y B, a la recta la corta en D.
Importante : Considerar el punto B el que está en el mismo lado que el punto P respecto de la recta y el punto A el que está en el lado contrario.
2 - Trazar una circunferencia que pase por B, D y el punto dado P.
3 - Unir P con A, donde corta a la circunferencia anterior es P'.
4 - El problema queda reducido reducido a : Dos puntos, P y P', y a la recta dada.
5 - Otra solución se obtiene si se traza una circunferencia que pase por A, D y P.
6 - Unir P con B, donde corta a la circunferencia anterior es P".
7 - El problema queda reducido a : Dos puntos, P y P", y a la recta dada.
Nota : En un caso genérico existiría otra solución que se obtiene si se traza una circunferencia que pase por A, D y P, se une P con B y donde corta a la circunferencia anterior es P". Quedando el problema reducido a : Dos puntos, P y P", y a la recta dada. Sin embargo, en este caso no es posible porque los dos puntos P y P" quedan a lados distintos de la recta y es imposible hallar una circunferencia que pase por los dos puntos y sea tangente a la recta.
Publicado: Sab, 12 Dic 2009, 17:33
por Fonsek
Yo la verdad que tampoco lo he logrado hacer, pero no se si lo hecho mal en este paso o en el siguiente
que lo hize siguiendo las indicaciones de aqui
viewtopic.php?p=3383#p3383
Publicado: Lun, 14 Dic 2009, 13:02
por julia segura
Hola:
Yo lo he solucionado utilizando la inversión.
He tomado como centro de inversión el punto dado que le he llamado P. Como razón de inversión he tomado el que deja la circunferencia dada invariable.
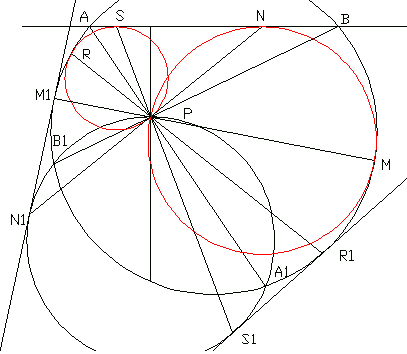
He hallado el inverso de la recta dada que es la circunferencia que pasa poe A1, B1 y P.Luego he dibujado las dos rectas tangentes con respecto a las dos circunferencias que tenemos . Los puntos de tangencia son R1y S1, y M1 y N1 respectivamente.
Las circunferencias solución son las que pasa por R,S y P una de ellas- Y la otra la que pasa por M,N y P.
Saludos
Publicado: Lun, 14 Dic 2009, 13:21
por Fonsek
Serias capaz de explicarlo con mas detalle? no soy capaz de hacer esas inversiones
Publicado: Mar, 15 Dic 2009, 09:21
por julia segura
Hola Fonsec:
Parto de la idea de que como las soluciones pasan por el centro de inversión, los inversos tienen que ser rectas. Por lo tanto tomo P como centro de inversión,y como razón de inversión aquella que deja la circunferencia dada invariable. El inverso de la recta dada es una circunferencia que pasa por el centro de inversión. Como se necesitan dos puntos más para dibujar la circunferencia, tomo los puntos A y B, que son comunes con la circunferencia dada. Los inversos de A y B tienen que estar en la circunferencia dada, ya que, como he dicho más arriba, he tomado una razón de inversión que deja la circunferencia dada invariable. Por lo tanto el inverso de la recta dada pasa por A1,B1 y P.
Como los inversos de las soluciones tienen que ser rectas,y además tangentes con las dos circunferencias, dibujo las dos tangentes comunes. Los puntos de tangencia son R1,S1,M1 y N1. El punto original de R1 tiene que encontrarse en la circunferencia dada, el punto original de S1 tiene que encontrarse en la recta dada, el punto original de M1 tiene que eencontrarse en la circunferencia dada, y el punto original de N1 tiene que encontrarse en la recta dada.
Por lo tanto las dos circunferencias solución tienen que pasar por M,N y P, y por R,S y P respectivamente.
No sé si habrá quedado muy claro.
Saludos
Ejercicio por Potencia CPR
Publicado: Dom, 20 Nov 2016, 09:04
por Alicantropo
Estoy buscando ejercicios para mis alumnos donde pudieran aplicar la resolución de tangencias por potencias y me he encontrado con este.
Mi problema es que yo solo he podido resolver desde aquí:
5 – Otra solución se obtiene si se traza una circunferencia que pase por B, D y P.
¿Cómo se resuelve la primera parte?
Un saludo
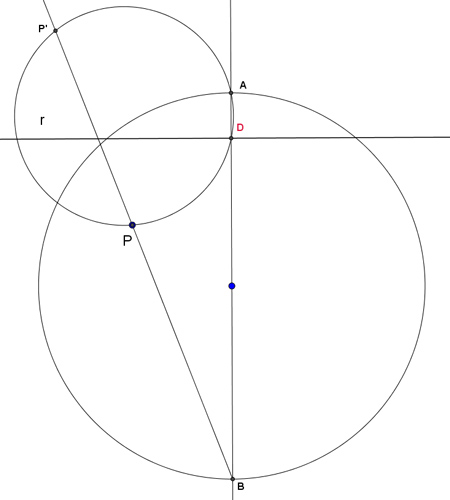
- Sin-título-2.jpg (24.7 KiB) Visto 2227 veces
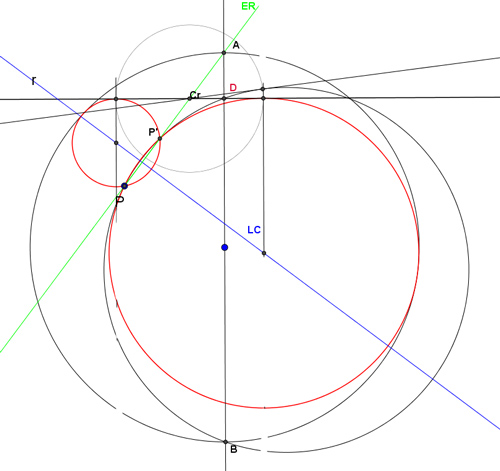
- Sin-título-3.jpg (59.55 KiB) Visto 2227 veces
Publicado: Dom, 20 Nov 2016, 12:01
por Antonio Castilla
.
Hola, Alicantropo.
La segunda solución que indiqué era para un caso genérico, pero llevado a determinados casos no existe esa segunda solución.
Ese es tu caso. Ten en cuenta que el problema lo hemos reducido a buscar las "circunferencias que pasen por P y P' (en tu primer dibujo) y sean tangentes a la recta R. Pero P y P' están en lados distintos de la recta R, luego, es imposible hallar una circunferencia que pase por los dos puntos sin atravesar la recta.
Por lo tanto, en este caso solo hay dos soluciones posibles en vez de las cuatro del caso genérico.
Esto que te ha ocurrido es muy habitual en los problemas de tangencia, por eso siempre hay que comprobar si verdaderamente es posible resolverlo en el caso particular que nos ocupe.
Pondré una advertencia en la solución para que otros usuarios no se vuelvan locos buscando la segunda solución.
Publicado: Dom, 20 Nov 2016, 12:06
por Alicantropo
Muchas gracias Antonio. Eso mismo me pareció a mí.
Un saludo


