hallar el centro de homología y el eje, con los cuales el homólogo del triangulo A1, B1, C1, es un triangulo isósceles de hipotenusa B2C2= 6 cm.
dibujar A2B2C2:
datos: A1(9;13), B1(11;16), C1(7;17'5) coordenadas en cm, L1: recta de ecuación "y = 20cm"
-Papel vertical. Origen de coordenadas el vertice inferior izquiero del recuadro.
gracias de antemano!!
problema de homologia
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
Hallar el centro de homología, el eje, y el homólogo con los cuales el homólogo del triángulo ABC, es un triángulo rectángulo isósceles de hipotenusa B'C' = 60 mm. A (90, 130), B (110, 160), C (70, 175). Recta límite R.L. de ecuación y = 200 mm.
1 - Prolongar los lados AB y AC hasta cortar a la recta límite, puntos X e Y.
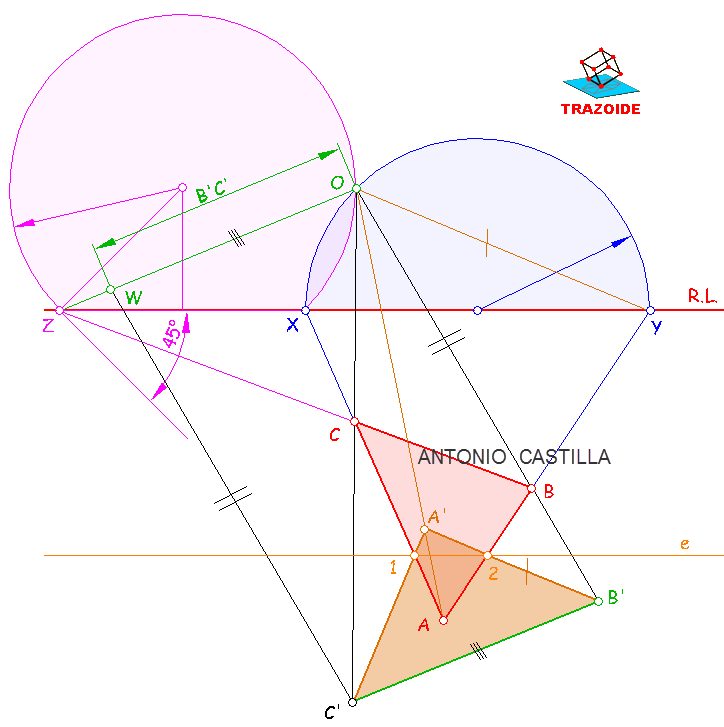
2 – Con centro en el punto medio de XY y diámetro XY dibujar una semicircunferencia por encima de la recta límite.
3 – Prolongar el lado BC hasta cortar a la recta límite, punto Z. Trazar el arco capaz de 45º por encima de la recta límite entre XZ.
4 – Donde se corten los dos arcos es el centro de homología, O.
Existe una segunda solución si se hacen los arcos por debajo de la recta límite, que no he dibujado.
5 – Unir el punto Z con el centro de homología O y sobre ella y a partir del centro se mide la longitud del lado B’C’, punto W.
6 – Unir el centro de homología O con los puntos B y C.
7 – Desde W trazar una paralela a OB y donde corte a OC es el primer punto transformado, C’.
8 – Por C’ hacer una paralela a OZ y donde corte a OB es el transformado B’.
9 – Unir Y con O y después una paralela a OY por B’. Donde corte a la unión de O con A es el último transformado A’.
10 – Uniendo los puntos de corte de los lados homólogos, AC con A’C’ y AB con A’B’, se obtiene el eje de homología.
Hallar el centro de homología, el eje, y el homólogo con los cuales el homólogo del triángulo ABC, es un triángulo rectángulo isósceles de hipotenusa B'C' = 60 mm. A (90, 130), B (110, 160), C (70, 175). Recta límite R.L. de ecuación y = 200 mm.
1 - Prolongar los lados AB y AC hasta cortar a la recta límite, puntos X e Y.

2 – Con centro en el punto medio de XY y diámetro XY dibujar una semicircunferencia por encima de la recta límite.
3 – Prolongar el lado BC hasta cortar a la recta límite, punto Z. Trazar el arco capaz de 45º por encima de la recta límite entre XZ.
4 – Donde se corten los dos arcos es el centro de homología, O.
Existe una segunda solución si se hacen los arcos por debajo de la recta límite, que no he dibujado.
5 – Unir el punto Z con el centro de homología O y sobre ella y a partir del centro se mide la longitud del lado B’C’, punto W.
6 – Unir el centro de homología O con los puntos B y C.
7 – Desde W trazar una paralela a OB y donde corte a OC es el primer punto transformado, C’.
8 – Por C’ hacer una paralela a OZ y donde corte a OB es el transformado B’.
9 – Unir Y con O y después una paralela a OY por B’. Donde corte a la unión de O con A es el último transformado A’.
10 – Uniendo los puntos de corte de los lados homólogos, AC con A’C’ y AB con A’B’, se obtiene el eje de homología.
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 26 invitados

