Hola a todos.
Estoy preparando un examen de dibujo y me he quedado encallado en un problema. Os pediría un poco de ayuda, puesto que le doy vueltas y no se me ocurre. Dice así:
La figura homológica de un paralelogramo ABCM con lados de igual longitud y valor del lado 6 cm es un cuadrilátero A'B'C'M'. Se conoce A' (0,0) B' (5,0) C' (4,5) M' (2,3). Definir el sistema de homología, indicando su centro, las rectas límites y el eje. El centro de homología queda lo más a la izquierda posible.
Muchas gracias de antemano y un saludo!
figura homológica de un paralelogramo
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
-
Contrainca12
- USUARIO

- Mensajes: 2
- Registrado: Vie, 01 Abr 2016, 16:54
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
1 - Situar los puntos A'B'C'D'.
En el enunciado original eran A'B'C'M', pero he cambiado la letra M' por D', que me gusta más.
No especificas dónde está el origen de coordenadas. Yo lo he colocado en la parte inferior izquierda.
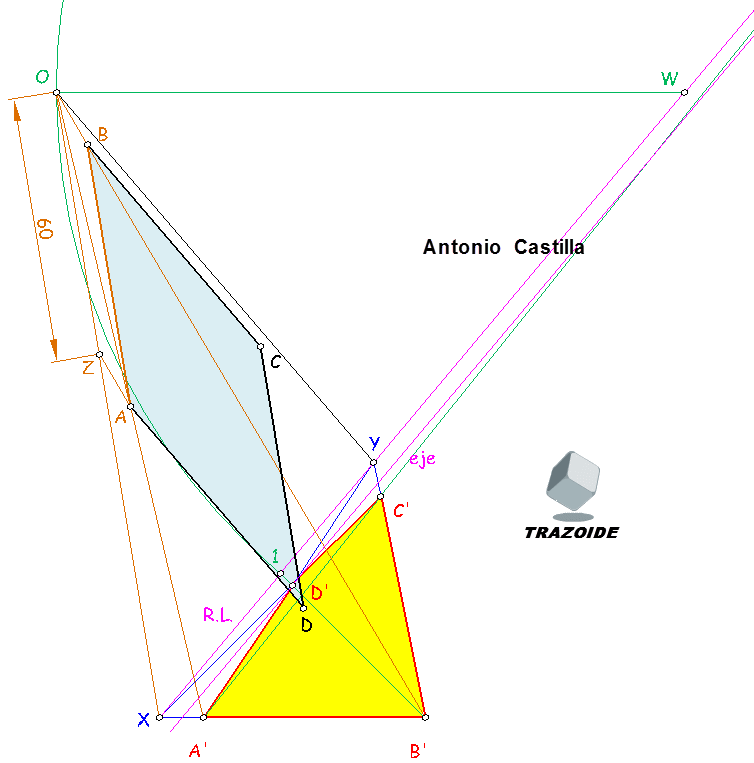
2 - Prolongar A'B' y C'D' hasta cortarse (punto X).
3 - Prolongar B'C' y A'D' hasta cortarse (punto Y).
4 - Uniendo X e Y tenemos la recta límite, R.L.
5 - Unir B' con D' hasta cortar a la recta límite en 1.
6 - Unir A' con C' hasta cortar a la recta límite en 2.
El punto 2 sale bastante alejado, pero el procedimiento es así. En la siguiente imagen se ve donde cae, aunque es mejor seguir la explicación con la imagen anterior en la que se ve todo más ampliado.
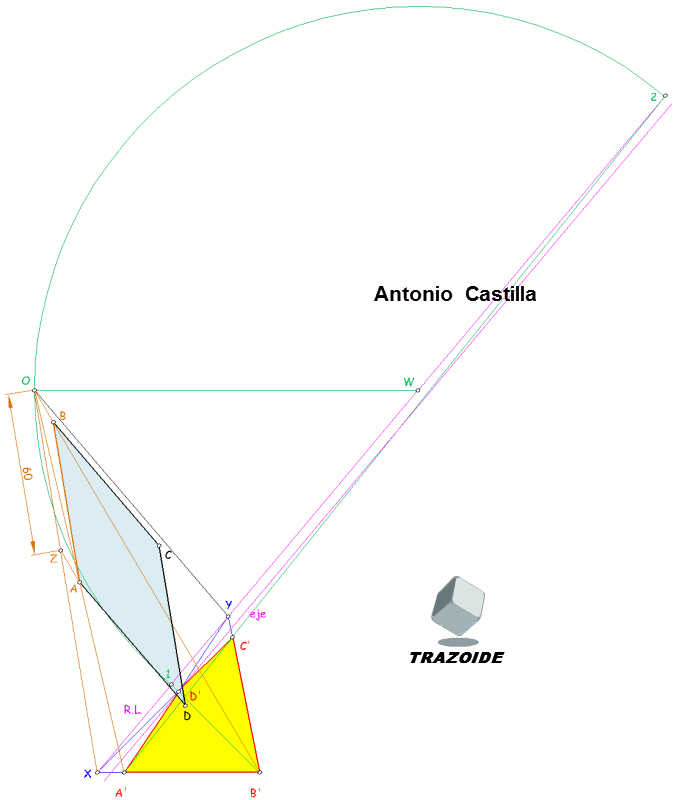
7 - Dibujar una semicircunferencia con diámetro 1-2. Al centro de la semicircunferencia lo he llamado W.
8 - Por el centro de la semicircunferencia, W, trazar una horizontal y donde la corte es el centro de la homología, O.
9 - Unir A' y B' con O. Unir X con O.
10 - Sobre OX y desde O medimos el valor del lado, 60 mm, obteniendo el punto Z.

11 - Por Z trazar una paralela a OB' y donde corte a OA' es el vértice A del paralelogramo buscado.
12 - Por A dibujar una paralela a OX y donde corta a OB' es el segundo vértice B.
13 - Unir O con Y. Por A trazar una paralela a OY y desde A medir el valor del lado del paralelogramo, 60 mm, obteniendo el vértice D, o si no se quiere medir esa distancia, unir D' con O y donde corte a la paralela de OY es D.
14 - Por D dibujar una paralela a AB y por B una paralela a AD. Donde ambas se corten es el último vértice C.
15 - El eje de la homología se logra con una paralela a la recta límite por donde se corten, por ejemplo, AD con A'D'.
1 - Situar los puntos A'B'C'D'.
En el enunciado original eran A'B'C'M', pero he cambiado la letra M' por D', que me gusta más.
No especificas dónde está el origen de coordenadas. Yo lo he colocado en la parte inferior izquierda.

2 - Prolongar A'B' y C'D' hasta cortarse (punto X).
3 - Prolongar B'C' y A'D' hasta cortarse (punto Y).
4 - Uniendo X e Y tenemos la recta límite, R.L.
5 - Unir B' con D' hasta cortar a la recta límite en 1.
6 - Unir A' con C' hasta cortar a la recta límite en 2.
El punto 2 sale bastante alejado, pero el procedimiento es así. En la siguiente imagen se ve donde cae, aunque es mejor seguir la explicación con la imagen anterior en la que se ve todo más ampliado.

7 - Dibujar una semicircunferencia con diámetro 1-2. Al centro de la semicircunferencia lo he llamado W.
8 - Por el centro de la semicircunferencia, W, trazar una horizontal y donde la corte es el centro de la homología, O.
9 - Unir A' y B' con O. Unir X con O.
10 - Sobre OX y desde O medimos el valor del lado, 60 mm, obteniendo el punto Z.

11 - Por Z trazar una paralela a OB' y donde corte a OA' es el vértice A del paralelogramo buscado.
12 - Por A dibujar una paralela a OX y donde corta a OB' es el segundo vértice B.
13 - Unir O con Y. Por A trazar una paralela a OY y desde A medir el valor del lado del paralelogramo, 60 mm, obteniendo el vértice D, o si no se quiere medir esa distancia, unir D' con O y donde corte a la paralela de OY es D.
14 - Por D dibujar una paralela a AB y por B una paralela a AD. Donde ambas se corten es el último vértice C.
15 - El eje de la homología se logra con una paralela a la recta límite por donde se corten, por ejemplo, AD con A'D'.
-
Contrainca12
- USUARIO

- Mensajes: 2
- Registrado: Vie, 01 Abr 2016, 16:54
Muchas gracias
Muchas gracias, Antonio. Entiendo que has dedicado un tiempo a resolver el ejercicio, que está perfectamente explicado, y te lo agradezco mucho.
Llegué hasta aquí, por recomendación de una usuaria, y pienso recomendar, yo también, esta web.
De nuevo, gracias y un saludo.
Llegué hasta aquí, por recomendación de una usuaria, y pienso recomendar, yo también, esta web.
De nuevo, gracias y un saludo.
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 38 invitados

