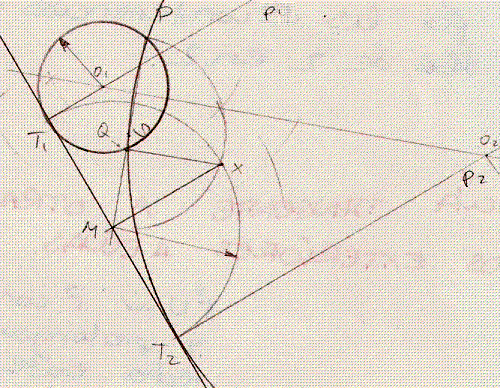
1º Unir los puntos hasta que corte la rectas
2º Media Proporcional por sustracción de los segmentos [PM] y[QM]
3º Centro en M, abertura media proporcional [XM] Trazar semicircunferencia T1 y T2
2 perpendiculares a la recta "s" que pasen por T1 y T2.
4º Mediatriz de [PQ]
5º Puntos de corte de la mediatriz m con las perpendiculares (P1 y P2) son los centros de las circunferencias que buscamos.

 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado


