Tetraedro y sombras
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
- caminante89
- CONTRIBUIDOR+

- Mensajes: 38
- Registrado: Lun, 18 Ago 2008, 12:40
Tetraedro y sombras
De un tetraedro regular se conoce la proyección horizontal de la arista AB, A1 (-2; 6; 0) B1 (2; 4; 0), y se sabe que la proyección horizontal de la arista BC, B1C1, es perpendicular a A1 B1 y que la traza horizontal del plano que contiene a la cara ABC contiene el punto M(6; 0; 0) y forma un ángulo de 60º con la línea de tierra en sentido antihorario.
Se pide: 1º. Representar las proyecciones del poliedro.
2º. Determinar la sombra propia y arrojada sobre los planos de proyección con luz paralela, cuyas proyecciones forman ángulos de 45º con la línea de tierra y descienden de izquierda a derecha.
NOTAS: Lámina en posición peraltada. Cotas en centímetros. Origen de coordenadas a 6 cm del borde izquierdo y a 15 cm del borde inferior.
Me interesa más la primera parte, la segunda parte se hacerla, no obstante si alguién supiera contestarme a la segunda pregunta de esta otra manera lo agradecería: Determinar la sombra propia y arrojada sobre los planos de proyección y el plano P(6, 5, 8) con luz paralela, cuyas proyecciones forman ángulos de 45º con la linea de tierra y desciendea de izquierda a derecha.
Gracias de antemano
Se pide: 1º. Representar las proyecciones del poliedro.
2º. Determinar la sombra propia y arrojada sobre los planos de proyección con luz paralela, cuyas proyecciones forman ángulos de 45º con la línea de tierra y descienden de izquierda a derecha.
NOTAS: Lámina en posición peraltada. Cotas en centímetros. Origen de coordenadas a 6 cm del borde izquierdo y a 15 cm del borde inferior.
Me interesa más la primera parte, la segunda parte se hacerla, no obstante si alguién supiera contestarme a la segunda pregunta de esta otra manera lo agradecería: Determinar la sombra propia y arrojada sobre los planos de proyección y el plano P(6, 5, 8) con luz paralela, cuyas proyecciones forman ángulos de 45º con la linea de tierra y desciendea de izquierda a derecha.
Gracias de antemano
Hola,
El tetraedro que te piden cumple dos requisitos,
_ En PHP se forma un cuadrado como contorno aparente del poliedro (recuerda que nos dicen que la proyección de la arista AB es perpendicular a su análoga BC). Esto nos lleva a pensar que dos de sus aristas son horizontales.
_ En PVP, la distancia que separa a estas dos aristas horizontales es la distancia mínima entre dos aristas opuestas. La hallamos dibujando un triángulo rectángulo en el que uno de sus catetos es la semiarista y la hipotenusa, la altura de la cara, siendo el otro cateto la distancia buscada.
SEGUIR LEYENDO EL RESTO DE LOS MENSAJES, YA QUE ESTE RAZONAMIENTO NO ES CORRECTO.
El tetraedro que te piden cumple dos requisitos,
_ En PHP se forma un cuadrado como contorno aparente del poliedro (recuerda que nos dicen que la proyección de la arista AB es perpendicular a su análoga BC). Esto nos lleva a pensar que dos de sus aristas son horizontales.
_ En PVP, la distancia que separa a estas dos aristas horizontales es la distancia mínima entre dos aristas opuestas. La hallamos dibujando un triángulo rectángulo en el que uno de sus catetos es la semiarista y la hipotenusa, la altura de la cara, siendo el otro cateto la distancia buscada.
SEGUIR LEYENDO EL RESTO DE LOS MENSAJES, YA QUE ESTE RAZONAMIENTO NO ES CORRECTO.
"Ahora puedo decirte que tomé la decisión correcta, sin embargo no hay un día que pase sin arrepentirme de no haber tomado una opción diferente".
- caminante89
- CONTRIBUIDOR+

- Mensajes: 38
- Registrado: Lun, 18 Ago 2008, 12:40
-
AlexPanda5
- USUARIO

- Mensajes: 1
- Registrado: Mié, 29 Feb 2012, 13:55
Tetraedro y sombras
Buenas. Alguien puede adjuntar un dibujo o una explicación más detallada del primer apartado, por favor? Gracias un saludo
-
AlexPanda5
- USUARIO

- Mensajes: 1
- Registrado: Mié, 29 Feb 2012, 13:55
Tetraedro y sombras
Siento repetir mensaje en el post, pero prefiero explicar bien mi duda.
Entiendo que la proyeccion horizontal es un cuadrado por la perpendicularidad de las aristas AB y BC.
Sin embargo la condición de que la traza horizontal del plano forme 60 grados con LT, hace que la supuesta arista horizontal AC no pueda formar parte de dicho plano. Por otro lado no conocemos la cota de ningún elemento. Cuál es el punto de partida para colocar la mínima distancia entre aristas horizontales? Gracias de nuevo
Entiendo que la proyeccion horizontal es un cuadrado por la perpendicularidad de las aristas AB y BC.
Sin embargo la condición de que la traza horizontal del plano forme 60 grados con LT, hace que la supuesta arista horizontal AC no pueda formar parte de dicho plano. Por otro lado no conocemos la cota de ningún elemento. Cuál es el punto de partida para colocar la mínima distancia entre aristas horizontales? Gracias de nuevo
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
Se ha hecho una suposición que no es correcta. El que la proyección horizontal de dos aristas sea perpendicular no significa que obligatoriamente las otras dos aristas sean paralelas a un plano de proyección, ese es solo un caso especial.
Así que olvidando esa suposición el ejercicio se resolvería así :
1 - Situamos las proyecciones horizontales de A y B, y una perpendicular a ella que será la recta soporte de la proyección horizontal de BC.
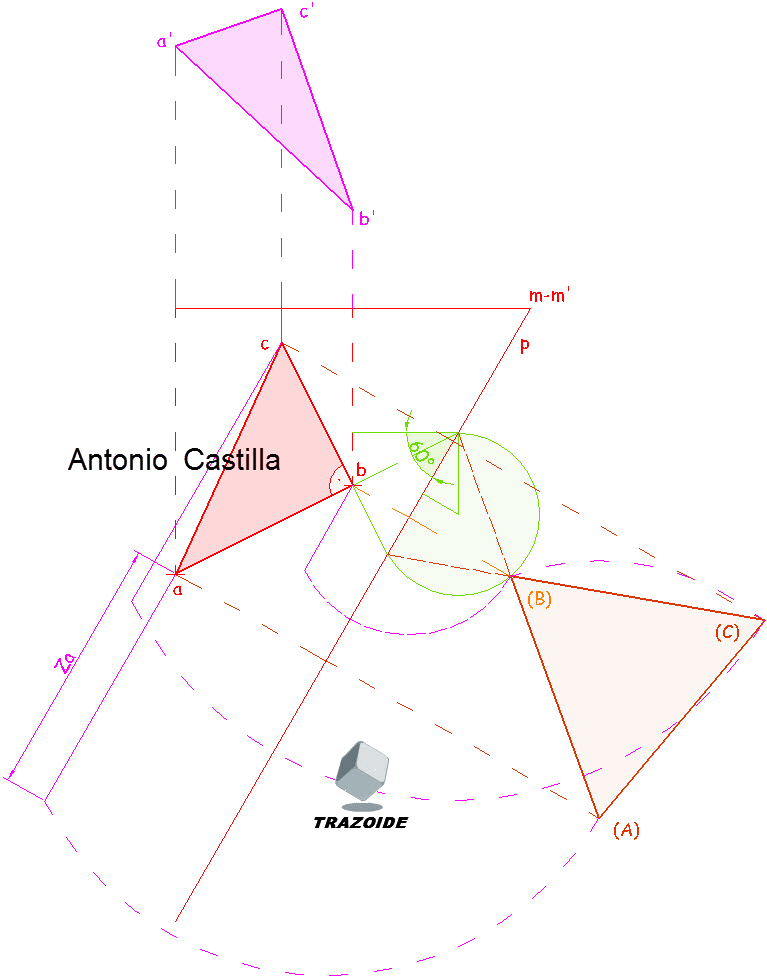
2 - Colocar el punto M y la traza horizontal del plano con el ángulo dado.
3 - Prolongar ab y bc hasta la traza del plano y dibujar el arco capaz de 60º respecto del segmento formado por las prolongaciones de esos dos lados con la traza.
4 - Desde la proyección horizontal de B se traza una perpendicular a la traza del plano y donde corte al arco capaz es el abatimiento de B.
5 - Unir B con donde las prolongaciones de ab y bc cortan a la traza del plano y esos son los lados AB y BC abatidos. El punto A abatido está donde la perpendicular a la traza del plano que pasa por a corta a estos lados.
6 - Conocidos A y B abatidos dibujar el triángulo equilátero.
7 - Conocidas las proyecciones horizontales y sus abatimientos determinar las cotas.
A partir de aquí imagino que no tendrás problema para dibujar el resto del tetraedro.
Se ha hecho una suposición que no es correcta. El que la proyección horizontal de dos aristas sea perpendicular no significa que obligatoriamente las otras dos aristas sean paralelas a un plano de proyección, ese es solo un caso especial.
Así que olvidando esa suposición el ejercicio se resolvería así :
1 - Situamos las proyecciones horizontales de A y B, y una perpendicular a ella que será la recta soporte de la proyección horizontal de BC.

2 - Colocar el punto M y la traza horizontal del plano con el ángulo dado.
3 - Prolongar ab y bc hasta la traza del plano y dibujar el arco capaz de 60º respecto del segmento formado por las prolongaciones de esos dos lados con la traza.
4 - Desde la proyección horizontal de B se traza una perpendicular a la traza del plano y donde corte al arco capaz es el abatimiento de B.
5 - Unir B con donde las prolongaciones de ab y bc cortan a la traza del plano y esos son los lados AB y BC abatidos. El punto A abatido está donde la perpendicular a la traza del plano que pasa por a corta a estos lados.
6 - Conocidos A y B abatidos dibujar el triángulo equilátero.
7 - Conocidas las proyecciones horizontales y sus abatimientos determinar las cotas.
A partir de aquí imagino que no tendrás problema para dibujar el resto del tetraedro.
-
AlexPanda5
- USUARIO

- Mensajes: 1
- Registrado: Mié, 29 Feb 2012, 13:55
Tetraedro y sombras
Muchas gracias Antonio, pero, cual es el fundamento de usar el arco capaz para el abatimiento?
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
Tetraedro y sombras
.
a - Las caras de un tetraedro regular son triángulos equiláteros.
b - Los ángulos de un triángulo equilátero miden 60º.
c - En un abatimiento los ángulos están en verdadera magnitud.
d - Entre la proyección horizontal y el abatimiento existe una relación de afinidad ortogonal en la que el eje es la traza del plano.
e - En una afinidad si prolongas una recta donde corte al eje de afinidad (traza del plano) desde ese punto parte la recta afín (abatida).
f - Si prolongas ab y bc hasta la traza del plano sus rectas abatidas (A)(B) y (B)(C) partirán de esos mismos puntos.
g - Las rectas abatidas (A)(B) y (B)(C) formarán un ángulo de 60º, por formar el vértice de un triángulo equilátero que en abatimiento está en verdadera magnitud.
h - Uniéndolo todo. Si construimos un arco capaz de 60º entre los puntos donde las proyecciones horizontales de ab y bc corten a la traza del plano, se tienen los infinitos puntos (lugar geométrico) que unidos con ellos forman un ángulo de 60º. Luego el vértice B abatido estará sobre dicho arco y como la afinidad es ortogonal estará donde la perpendicular a la traza del plano que parte de b corte al arco.
a - Las caras de un tetraedro regular son triángulos equiláteros.
b - Los ángulos de un triángulo equilátero miden 60º.
c - En un abatimiento los ángulos están en verdadera magnitud.
d - Entre la proyección horizontal y el abatimiento existe una relación de afinidad ortogonal en la que el eje es la traza del plano.
e - En una afinidad si prolongas una recta donde corte al eje de afinidad (traza del plano) desde ese punto parte la recta afín (abatida).
f - Si prolongas ab y bc hasta la traza del plano sus rectas abatidas (A)(B) y (B)(C) partirán de esos mismos puntos.
g - Las rectas abatidas (A)(B) y (B)(C) formarán un ángulo de 60º, por formar el vértice de un triángulo equilátero que en abatimiento está en verdadera magnitud.
h - Uniéndolo todo. Si construimos un arco capaz de 60º entre los puntos donde las proyecciones horizontales de ab y bc corten a la traza del plano, se tienen los infinitos puntos (lugar geométrico) que unidos con ellos forman un ángulo de 60º. Luego el vértice B abatido estará sobre dicho arco y como la afinidad es ortogonal estará donde la perpendicular a la traza del plano que parte de b corte al arco.
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 123 invitados



