Angulo entre dos planos
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
Angulo entre dos planos
Hola, de manera general para dos planos oblicuos ¿como se puede hallar el angulo que forman?
Preferiblemente sin cambios de plano
Preferiblemente sin cambios de plano
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
Ángulo formado por dos planos, P y Q (sin utilizar cambios de plano) Primera opción.
1 - Elegir un punto cualquiera, A
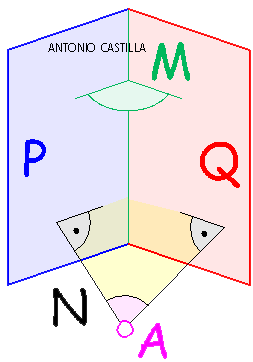
2 - Trazar desde A dos rectas perpendiculares a los planos
3 - Las dos rectas perpendiculares forman un plano, abatir sendas rectas respecto del plano que forman
4 - En el abatimiento se mide la verdadera magnitud del ángulo formado por las dos rectas, N
5 - El ángulo entre los dos planos, M, es el suplementario del ángulo entre las dos rectas, M = 180º - N
Ángulo formado por dos planos, P y Q (sin utilizar cambios de plano) Primera opción.
1 - Elegir un punto cualquiera, A

2 - Trazar desde A dos rectas perpendiculares a los planos
3 - Las dos rectas perpendiculares forman un plano, abatir sendas rectas respecto del plano que forman
4 - En el abatimiento se mide la verdadera magnitud del ángulo formado por las dos rectas, N
5 - El ángulo entre los dos planos, M, es el suplementario del ángulo entre las dos rectas, M = 180º - N
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
Ángulo formado por dos planos, P y Q (sin utilizar cambios de plano) Segunda opción.
a - Hallar la intersección entre los dos planos, I
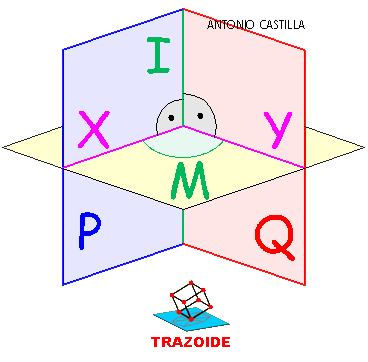
b - Dibujar un plano perpendicular a la intersección de los dos planos, I, en cualquier lugar
c - Hallar las intersecciones, X e Y, del plano perpendicular con los dos planos dados, P y Q
d - Abatir las dos rectas intersección, X e Y, respecto del plano perpendicular
e - El ángulo, M, formado por las dos rectas X e Y abatidas es el ángulo formado por los dos planos
Ángulo formado por dos planos, P y Q (sin utilizar cambios de plano) Segunda opción.
a - Hallar la intersección entre los dos planos, I

b - Dibujar un plano perpendicular a la intersección de los dos planos, I, en cualquier lugar
c - Hallar las intersecciones, X e Y, del plano perpendicular con los dos planos dados, P y Q
d - Abatir las dos rectas intersección, X e Y, respecto del plano perpendicular
e - El ángulo, M, formado por las dos rectas X e Y abatidas es el ángulo formado por los dos planos
hola a todos ¡¡
Me e puesto dos planos oblicuos para practicar estos métodos y me he encontrado a qui parado y no se seguir, hago las dos rectas intersección, el plano que forman pero a la hora de abatir una de ellas me encuentro con que me sale muy rara, no me queda claro ni que concuerde la recta que en principio esta el el primer cuadrante con la posición del plano.
Os adjunto foto con la parte en la que me he quedado atrapado repetida a ver si alguien me puede decir si me he equivocado o si no, y como seguir o direccionarme a un punto del foro donde se explique este caso.
Muchas gracias
Me e puesto dos planos oblicuos para practicar estos métodos y me he encontrado a qui parado y no se seguir, hago las dos rectas intersección, el plano que forman pero a la hora de abatir una de ellas me encuentro con que me sale muy rara, no me queda claro ni que concuerde la recta que en principio esta el el primer cuadrante con la posición del plano.
Os adjunto foto con la parte en la que me he quedado atrapado repetida a ver si alguien me puede decir si me he equivocado o si no, y como seguir o direccionarme a un punto del foro donde se explique este caso.
Muchas gracias
- fernandore
- MODERADOR++

- Mensajes: 2093
- Registrado: Mar, 03 Jun 2008, 22:27
1-Yo hubirera tomado otro punto A desde donde trazar las perpendiculares a los planos.Porq el q has tomado hace q el dibujo quede con muy poco espacio para dibujar (de ahí naceran imprecisiones q luego se arrastran durante todo el ejercicio)
2-Al calcular las trazas del plano ganma has cometido un error ya q "tu" traza vertical es en realidad la traza horizontal (ocurre q las trazas horizontales de las rectas te salen en el en el segundo cuadrante y eso te ha inducido al error)
3-Cuando abatas las rectas R y S,observa q solo necesitas abatir el punto intersección,los otros 2 puntos tomalos de los cortes de las rectas con la charnela
Salu2
2-Al calcular las trazas del plano ganma has cometido un error ya q "tu" traza vertical es en realidad la traza horizontal (ocurre q las trazas horizontales de las rectas te salen en el en el segundo cuadrante y eso te ha inducido al error)
3-Cuando abatas las rectas R y S,observa q solo necesitas abatir el punto intersección,los otros 2 puntos tomalos de los cortes de las rectas con la charnela
Salu2
Hola ¡¡¡¡
Pues aquí e vuelto a pillar este ejercicio, me he empecinado con el ... Veo ahora claro mi error y las trazas del plano. Lo he vuelto a repetir y por su posición me planteo el abatimiento sobre el plano vertical, y plas¡ me e vuelto a dar en la cabeza y pararme a pensar.
Para intentar entenderlo me he dibujado uno parecido y he intentado colocar una recta horizonal en el, y abatir un punto de ella que este en el 1er cuadrante sobre PVP. Tengo bastante dudas sobre si es correcto lo que he hecho.
Que le parece Fernadore?
Gracias de antemano.
Pues aquí e vuelto a pillar este ejercicio, me he empecinado con el ... Veo ahora claro mi error y las trazas del plano. Lo he vuelto a repetir y por su posición me planteo el abatimiento sobre el plano vertical, y plas¡ me e vuelto a dar en la cabeza y pararme a pensar.
Para intentar entenderlo me he dibujado uno parecido y he intentado colocar una recta horizonal en el, y abatir un punto de ella que este en el 1er cuadrante sobre PVP. Tengo bastante dudas sobre si es correcto lo que he hecho.
Que le parece Fernadore?
Gracias de antemano.
- fernandore
- MODERADOR++

- Mensajes: 2093
- Registrado: Mar, 03 Jun 2008, 22:27
yo si que lo siento que veo que doy mucho mal...
Bueno, he intentedo hacer en el dibujo de la derecha un plano alpha con la traza horizontal en el 2º cuadrante, y luego e intentado colocar un punto "A"y por el una recta horizontal del plano para ver como quedaria, y finalmente abatir ese punto sobre el PVP.
Ya imagino por su respuesta que hay tragedia en el intento..
Gracias
Bueno, he intentedo hacer en el dibujo de la derecha un plano alpha con la traza horizontal en el 2º cuadrante, y luego e intentado colocar un punto "A"y por el una recta horizontal del plano para ver como quedaria, y finalmente abatir ese punto sobre el PVP.
Ya imagino por su respuesta que hay tragedia en el intento..
Gracias
- fernandore
- MODERADOR++

- Mensajes: 2093
- Registrado: Mar, 03 Jun 2008, 22:27
Vale ya lo he pillado,es q me despistaba la recta q has llamado alfa (paralela a la charnela).
El abatimiento está correcto.
Una puntualizacion.Todos los planos oblicuos (ecepto lo paralelos a la LT) tienen su traza horizontal, parte en el primer cuadrante y parte en el segundo cuadrante.Lo q ocurre q solo se dibuja la parte correspondiente al primer cuadrante.
Salu2
El abatimiento está correcto.
Una puntualizacion.Todos los planos oblicuos (ecepto lo paralelos a la LT) tienen su traza horizontal, parte en el primer cuadrante y parte en el segundo cuadrante.Lo q ocurre q solo se dibuja la parte correspondiente al primer cuadrante.
Salu2
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 95 invitados

