.
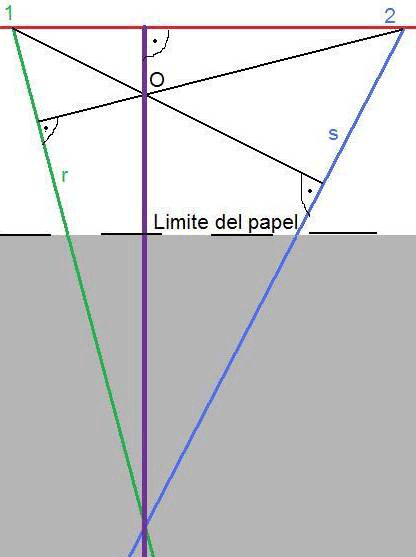
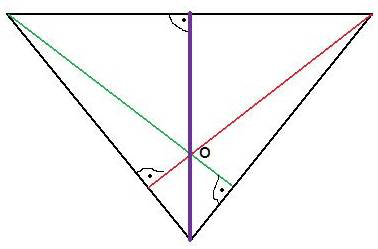
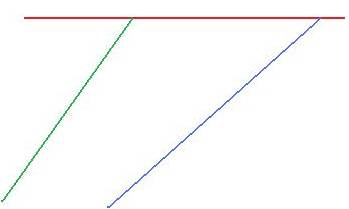
Trazar una recta perpendicular a la recta R que pase por el punto de corte de otras dos, S y T, estando el punto de corte fuera de los límites del papel
1 - Dibujar una paralela, S', a la recta S en un lugar cualquiera, pero que corte a la recta T dentro de los límites del papel
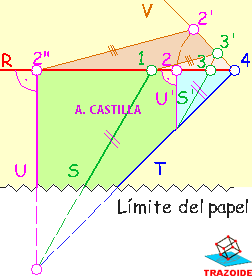
2 - Por el punto de corte de ambas, S' y T, se traza una perpendicular, U', a R.
3 - Las rectas S, U', S' y T cortan a R en los puntos 1, 2, 3 y 4 respectivamente. Por el punto 4 hacer una recta, V, cualquiera (también se puede utilizar la recta T, pero he preferido hacer otra para mayor claridad)
4 - Llevar sobre la nueva recta, V, las distancias 2-4 y 3-4, obteniendo los puntos 2' y 3'
5 - Unir 1 con 3' y dibujar una paralela a ella por 2'. Esto nos da el punto 2" sobre R
6 - El punto 2" es el pie de la perpendicular buscada, U. Trazar por 2" una perpendicular a R

 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado