TRIÁNGULO ISÓSCELES CONOCIDO MEDIANA Y ALTURA
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
TRIÁNGULO ISÓSCELES CONOCIDO MEDIANA Y ALTURA
Hola buenas, el enunciado del problema dice:
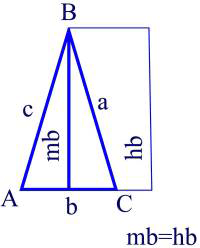
Dibujar triángulo isósceles conocido mb=30mm y hb=27 mm.
Muchas gracias por anticipado
Dibujar triángulo isósceles conocido mb=30mm y hb=27 mm.
Muchas gracias por anticipado
Hola, pues podría ser , sólo que para construir un triángulo se necesitan siempre 3 datos. Supongo que el tercer dato viene implícito (que la otra mediana mide lo mismo por ser un triángulo simétrico). Creo que necesitaremos ayuda del MAESTRO A. Castilla. Recordemos que las dos medianas dadas se cortan a sus 2/3. Intentaré resolverlo pero tengo mis limitaciones, siento no poder ayudarte más. Marta
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
Triángulo isósceles conocida la altura, hb, y la mediana, mb, respecto de un mismo vértice B.
1 - Dibujar una recta (horizontal en mi dibujo) y sobre ella en cualquier punto una perpendicular con la medida de la altura, XB = hb. El extremo B es uno de los vértices del triángulo.
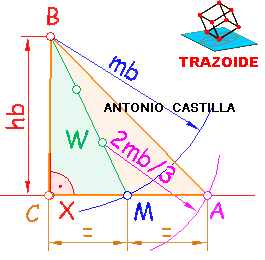
2 - Con centro en el extremo de la altura, B, y radio la mediana, mb, se traza un arco que corte a la recta inicial. Este punto, M, es el punto medio del lado b.
3 - Unir B con M y dividirlo en tres partes iguales.
4 - Tomar centro en la segunda división, W, a partir de B (baricentro) y con radio 2·mb/3 se dibuja un arco que corte a la línea inicial. El punto de corte, A, es el segundo vértice del triángulo.
5 - Sobre la recta inicial llevar la medida A-M hacia el otro lado y se consigue el tercer vértice C.
Nota : Con las medidas del problema el triángulo isósceles sale casi rectángulo, de ahí el que los puntos X y C o los segmentos XB y CB estén casi coincidentes.
Triángulo isósceles conocida la altura, hb, y la mediana, mb, respecto de un mismo vértice B.
1 - Dibujar una recta (horizontal en mi dibujo) y sobre ella en cualquier punto una perpendicular con la medida de la altura, XB = hb. El extremo B es uno de los vértices del triángulo.

2 - Con centro en el extremo de la altura, B, y radio la mediana, mb, se traza un arco que corte a la recta inicial. Este punto, M, es el punto medio del lado b.
3 - Unir B con M y dividirlo en tres partes iguales.
4 - Tomar centro en la segunda división, W, a partir de B (baricentro) y con radio 2·mb/3 se dibuja un arco que corte a la línea inicial. El punto de corte, A, es el segundo vértice del triángulo.
5 - Sobre la recta inicial llevar la medida A-M hacia el otro lado y se consigue el tercer vértice C.
Nota : Con las medidas del problema el triángulo isósceles sale casi rectángulo, de ahí el que los puntos X y C o los segmentos XB y CB estén casi coincidentes.
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 60 invitados