Hallar un hexágono regular equivalente a un pentágono regular
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
Hallar un hexágono regular equivalente a un pentágono regular
¡Hey! Tengo dudas en este problema. Dado un pentágono regular de lado AB=35 mm, se pide:
a) Dibujar un rectángulo equivalente que sus lados estén en proporción a/b= 3/1.
b) Dibujar un hexágono regular equivalente al péntagono anterior.
¡Gracias!
a) Dibujar un rectángulo equivalente que sus lados estén en proporción a/b= 3/1.
b) Dibujar un hexágono regular equivalente al péntagono anterior.
¡Gracias!
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
Rectángulo equivalente a un pentágono regular, estando la base y altura del rectángulo en un proporción de 3/1
Existen muchas formas de hacerlo :
OPCIÓN I
1 - El área del pentágono es 5·L·R/2 , donde L es la medida del lado y R el radio de la circunferencia inscrita. El área del rectángulo es b·h, donde b es su base y h su altura. Y entre la base y la altura del rectángulo b/h = 3/1, o bien, b = 3·h.
2 - Igualando las áreas 5·L·R/2 = b·h, y sustituyendo, 5·L·R/2 = (3·h)·h.
Reordenando, (5·L/6)·R = h·h.
3 - Plantear una media proporcional entre (5·L/6) y R, el resultado es h.
4 - Conseguido la altura, h, la base es b = 3·h
OPCIÓN II
5 - Reducir el pentágono a un triángulo equivalente. Pulsar aquí para ver el procedimiento.
6 - El área del triángulo es B·H/2. Si la igualamos a la del rectángulo B·H/2 = b·h, sustituyendo como antes, B·H/2 = (3·h)·h. Y reordenadolo, B·H/6 = h·h.
7 - Resolver la media proporcional de B y H/6 para obtener h.
Rectángulo equivalente a un pentágono regular, estando la base y altura del rectángulo en un proporción de 3/1
Existen muchas formas de hacerlo :
OPCIÓN I
1 - El área del pentágono es 5·L·R/2 , donde L es la medida del lado y R el radio de la circunferencia inscrita. El área del rectángulo es b·h, donde b es su base y h su altura. Y entre la base y la altura del rectángulo b/h = 3/1, o bien, b = 3·h.
2 - Igualando las áreas 5·L·R/2 = b·h, y sustituyendo, 5·L·R/2 = (3·h)·h.
Reordenando, (5·L/6)·R = h·h.
3 - Plantear una media proporcional entre (5·L/6) y R, el resultado es h.
4 - Conseguido la altura, h, la base es b = 3·h
OPCIÓN II
5 - Reducir el pentágono a un triángulo equivalente. Pulsar aquí para ver el procedimiento.
6 - El área del triángulo es B·H/2. Si la igualamos a la del rectángulo B·H/2 = b·h, sustituyendo como antes, B·H/2 = (3·h)·h. Y reordenadolo, B·H/6 = h·h.
7 - Resolver la media proporcional de B y H/6 para obtener h.
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
Hallar un hexágono regular equivalente a un pentágono regular.
a - El área pentágono es 5·L·A/2, donde L es la longitud del lado y A su apotema.
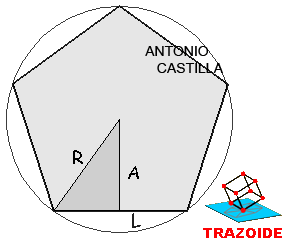
b - Se iguala al área de un cuadrado de lado X, 5·L·A/2 = X·X. Mediante una media proporcional de (5·L/2) y A se determina el lado X del cuadrado.
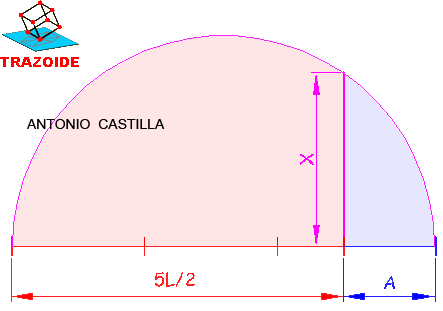
c - Se halla 4/9 del lado del cuadrado.
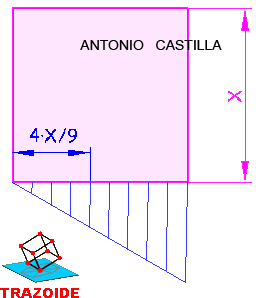
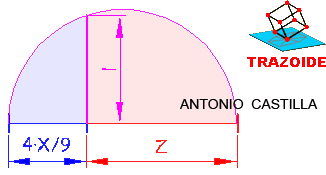
d - Se traza un ángulo de 90º y sobre uno de sus lados se lleva la mitad del lado del cuadrado, X/2. Con centro en su extremo y radio el lado del cuadrado, X, se corta a la perpendicular. El cateto formado es Z.
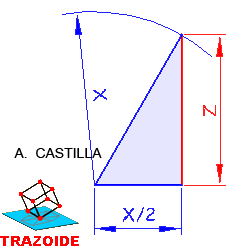
e - Se halla la media proporcional entre 4X/9 y Z. El resultado es el lado, l, del hexágono buscado.
Hallar un hexágono regular equivalente a un pentágono regular.
a - El área pentágono es 5·L·A/2, donde L es la longitud del lado y A su apotema.

b - Se iguala al área de un cuadrado de lado X, 5·L·A/2 = X·X. Mediante una media proporcional de (5·L/2) y A se determina el lado X del cuadrado.

c - Se halla 4/9 del lado del cuadrado.

d - Se traza un ángulo de 90º y sobre uno de sus lados se lleva la mitad del lado del cuadrado, X/2. Con centro en su extremo y radio el lado del cuadrado, X, se corta a la perpendicular. El cateto formado es Z.

e - Se halla la media proporcional entre 4X/9 y Z. El resultado es el lado, l, del hexágono buscado.

- iherrero20
- CONTRIBUIDOR+++

- Mensajes: 61
- Registrado: Vie, 20 Nov 2009, 15:37
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
Posiblemente haya una forma más sencilla, pero esa fue la que hice hace ya algún tiempo. Te pongo el razonamiento :
En un hexágono el triángulo formado por el radio, la apotema y el pie de la apotema, tiene por hipotenusa el radio que es igual al lado y por catetos medio lado y la apotema.
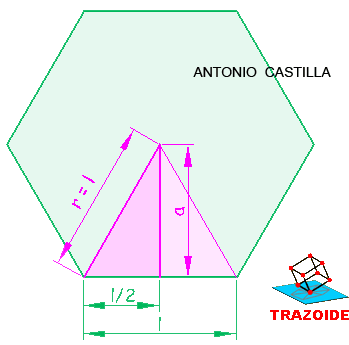
Por Pitágoras :
r = l
l² = a² + (l/2)²
a² = l² - (l²/4) = 3·l²/4
a = √(3·l²/4) = l·(√3)/2
Luego en la ecuación del área del hexágono podemos sustituir :
Área hexágono = 6·l·a/2 = 3·l·(l·(√3)/2) = 3·l·l·(√3)/2
Si se igualan el área del hexágono a la del cuadrado :
Área hexágono = Área pentágono = Área cuadrado
6·l·a/2 = 3·l·l·(√3)/2 =X·X
l·l = (2·X/3)·(X/√3) = (2·X/3)·(X·√3/√3·√3) = (2·X/3)·(X·√3/3) = (2·X/3)·(X·2·√3/2·3) = (2·2·X/3·3)·(X·√3/2) = (4·X/9)·Z
Z es el cateto de un triángulo rectángulo de hipotenusa el lado del cuadrado X y un cateto igual a la mitad del lado del cuadrado (deducido del triángulo del hexágono).
Luego se resuelve la media proporcional l·l = (4·X/9)·Z para obtener el lado del hexágono, l.
Posiblemente haya una forma más sencilla, pero esa fue la que hice hace ya algún tiempo. Te pongo el razonamiento :
En un hexágono el triángulo formado por el radio, la apotema y el pie de la apotema, tiene por hipotenusa el radio que es igual al lado y por catetos medio lado y la apotema.

Por Pitágoras :
r = l
l² = a² + (l/2)²
a² = l² - (l²/4) = 3·l²/4
a = √(3·l²/4) = l·(√3)/2
Luego en la ecuación del área del hexágono podemos sustituir :
Área hexágono = 6·l·a/2 = 3·l·(l·(√3)/2) = 3·l·l·(√3)/2
Si se igualan el área del hexágono a la del cuadrado :
Área hexágono = Área pentágono = Área cuadrado
6·l·a/2 = 3·l·l·(√3)/2 =X·X
l·l = (2·X/3)·(X/√3) = (2·X/3)·(X·√3/√3·√3) = (2·X/3)·(X·√3/3) = (2·X/3)·(X·2·√3/2·3) = (2·2·X/3·3)·(X·√3/2) = (4·X/9)·Z
Z es el cateto de un triángulo rectángulo de hipotenusa el lado del cuadrado X y un cateto igual a la mitad del lado del cuadrado (deducido del triángulo del hexágono).
Luego se resuelve la media proporcional l·l = (4·X/9)·Z para obtener el lado del hexágono, l.
- iherrero20
- CONTRIBUIDOR+++

- Mensajes: 61
- Registrado: Vie, 20 Nov 2009, 15:37
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 10 invitados


