Triangulo conociendo un lado, la suma de los otros dos y la altura del lado conocido
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
Triangulo conociendo un lado, la suma de los otros dos y la altura del lado conocido
Hola! ayer hice un examen de dibujo técnico y apareció el siguiente ejercicio, pero no supe resolverlo.
Construye un triangulo conociendo el lado a= 45mm, la suma de los otros dos lados b+c=92mm y la altura ha=38 mm.
Me gustaria saber también el razonamiento del ejercicio si no es mucha molestia, gracias.
y porcierto, felicitaciones por la pagina. A mi por lo menos me ayuda muchisimo.
Construye un triangulo conociendo el lado a= 45mm, la suma de los otros dos lados b+c=92mm y la altura ha=38 mm.
Me gustaria saber también el razonamiento del ejercicio si no es mucha molestia, gracias.
y porcierto, felicitaciones por la pagina. A mi por lo menos me ayuda muchisimo.
- julia segura
- MODERADOR+

- Mensajes: 604
- Registrado: Vie, 02 Ene 2009, 19:16
Hola Lourdes:
- Primero hallamos el radio de la circunferencia inscrita. Para hacerlo relacionamos dos fórmulas que nos sirven para calcular el área del triángulo: el producto de la base por la altura partido por dos y el producto del semiperímetro por el radio de la circunferencia inscrita.
a.h/2= p.r
Lo podemos solucionar numéricamete o bien gráficamente echando mano de la cuarta proporcional y del teorema de Thales. Para ello la anterior ecuación la transformamos en una proporción: a / 2p = r/h.
-Segundo calculamos el ángulo del vértice opuesto al lado a. La distancia que hay desde los puntos de tangencia de la circunfererencia inscrita hasta el vértice C es igual a (p-a).
- Ahora dibujamos el triángulo ya que conocemos el lado, el ángulo opuesto y la altura.
Saludos.
- Primero hallamos el radio de la circunferencia inscrita. Para hacerlo relacionamos dos fórmulas que nos sirven para calcular el área del triángulo: el producto de la base por la altura partido por dos y el producto del semiperímetro por el radio de la circunferencia inscrita.
a.h/2= p.r
Lo podemos solucionar numéricamete o bien gráficamente echando mano de la cuarta proporcional y del teorema de Thales. Para ello la anterior ecuación la transformamos en una proporción: a / 2p = r/h.
-Segundo calculamos el ángulo del vértice opuesto al lado a. La distancia que hay desde los puntos de tangencia de la circunfererencia inscrita hasta el vértice C es igual a (p-a).
- Ahora dibujamos el triángulo ya que conocemos el lado, el ángulo opuesto y la altura.
Saludos.
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
El procedimiento es como te ha explicado Julia, únicamente que ha cometido un pequeño error al escribir "hasta el vértice C es igual a (p-a).", la frase correcta es " hasta el vértice A es igual a (p-a)."
Tal vez por eso no te salía al pensar que conseguías el ángulo C cuando en realidad era el ángulo A.
Dentro de un rato te pongo un dibujo siguiendo los mismos pasos que te ha explicado Julia.
El procedimiento es como te ha explicado Julia, únicamente que ha cometido un pequeño error al escribir "hasta el vértice C es igual a (p-a).", la frase correcta es " hasta el vértice A es igual a (p-a)."
Tal vez por eso no te salía al pensar que conseguías el ángulo C cuando en realidad era el ángulo A.
Dentro de un rato te pongo un dibujo siguiendo los mismos pasos que te ha explicado Julia.
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
Construir un triángulo conociendo el lado a = 45 mm, la suma de los otros dos lados b + c = 92 mm y la altura ha = 38 mm.
1 - Hallar el perímetro, p, sumando a + (b + c) = p.
Cuidado con la nomenclatura, es habitual denominar al semiperímetro como p (así te lo ha explicado Julia), en ese caso el perímetro es 2p, pero yo llamaré al perímetro p y al semiperímetro p/2.
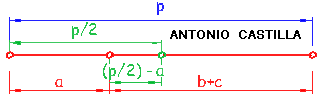
2 - Plantear la igualdad de áreas, a·h/2 = p·r/2, en la que "a" es el lado "a" o base del triángulo, h su altura, p el perímetro y r el radio de la circunferencia inscrita. Hallar r mediante una cuarta proporcional, a/p = r/h.
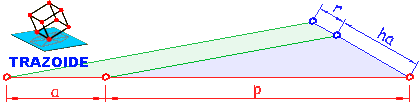
3 - Hallamos la diferencia, (p/2) - a, entre el semiperímetro, p/2, y el lado dado, a (en verde en el siguiente dibujo).

4 - Sobre una recta, A-Tc, colocamos el valor de esa diferencia y por uno de sus extremos y en perpendicular a ella el valor del radio, r, de la circunferencia inscrita.
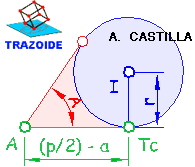
5 - A continuación hay dos posibles opciones, escoge la que creas mas rápida o sencilla :
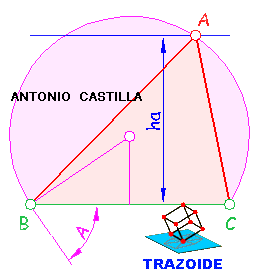
7 - Hacer una paralela al lado "a" a una distancia igual a su altura, ha.
8 - Donde se corten la paralela y el arco capaz es el vértice A.
9 - Unir A con B y C.
Construir un triángulo conociendo el lado a = 45 mm, la suma de los otros dos lados b + c = 92 mm y la altura ha = 38 mm.
1 - Hallar el perímetro, p, sumando a + (b + c) = p.
Cuidado con la nomenclatura, es habitual denominar al semiperímetro como p (así te lo ha explicado Julia), en ese caso el perímetro es 2p, pero yo llamaré al perímetro p y al semiperímetro p/2.

2 - Plantear la igualdad de áreas, a·h/2 = p·r/2, en la que "a" es el lado "a" o base del triángulo, h su altura, p el perímetro y r el radio de la circunferencia inscrita. Hallar r mediante una cuarta proporcional, a/p = r/h.

3 - Hallamos la diferencia, (p/2) - a, entre el semiperímetro, p/2, y el lado dado, a (en verde en el siguiente dibujo).

4 - Sobre una recta, A-Tc, colocamos el valor de esa diferencia y por uno de sus extremos y en perpendicular a ella el valor del radio, r, de la circunferencia inscrita.

5 - A continuación hay dos posibles opciones, escoge la que creas mas rápida o sencilla :
- Con el radio r y desde el extremo, I, de la perpendicular anterior se dibuja una circunferencia. Desde el otro extremo de la diferencia (p/2) - a se traza la tangente a la circunferencia. El ángulo que se forma entre el segmento A-Tc y la tangente es el ángulo A. (Este procedimiento es el que se ve en la figura anterior)
- Unir el extremo, I, de la perpendicular con el extremo A. El ángulo formado entre esta última y A-Tc es el semiángulo A, A/2. (Este caso no lo he dibujado)

7 - Hacer una paralela al lado "a" a una distancia igual a su altura, ha.
8 - Donde se corten la paralela y el arco capaz es el vértice A.
9 - Unir A con B y C.
- julia segura
- MODERADOR+

- Mensajes: 604
- Registrado: Vie, 02 Ene 2009, 19:16
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 49 invitados

