.
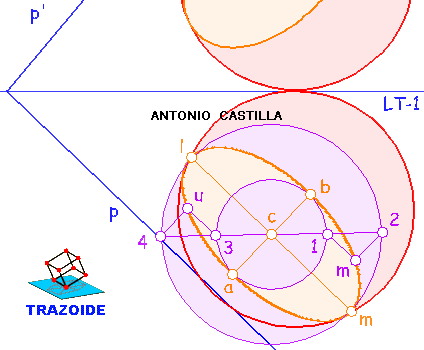
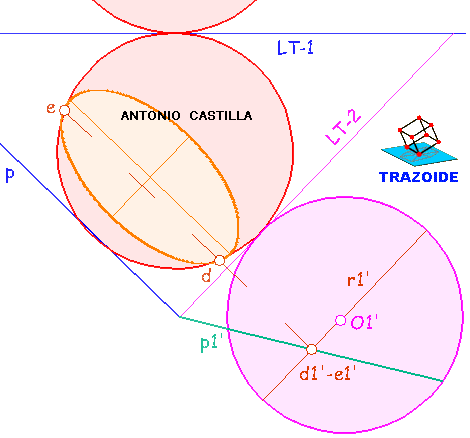
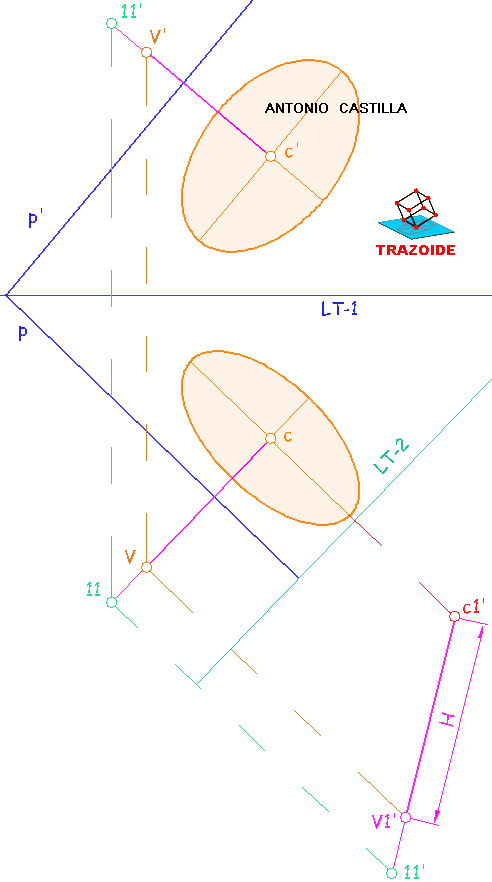
Sección de una esfera de centro O por un plano oblicuo P.
Determinación de los ejes principales (mayor y menor) de la elipse proyección de la sección, mediante cambios de plano
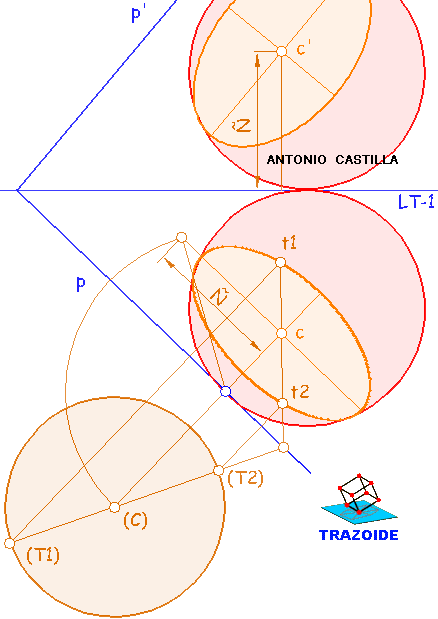
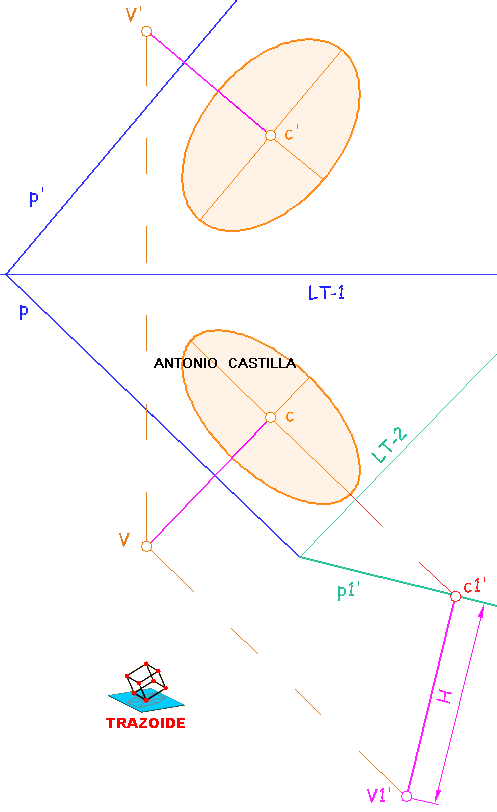
1 - Realizar un cambio de plano donde la segunda línea de tierra, LT-2, es perpendicular a la traza horizontal, p, del plano.
2 -
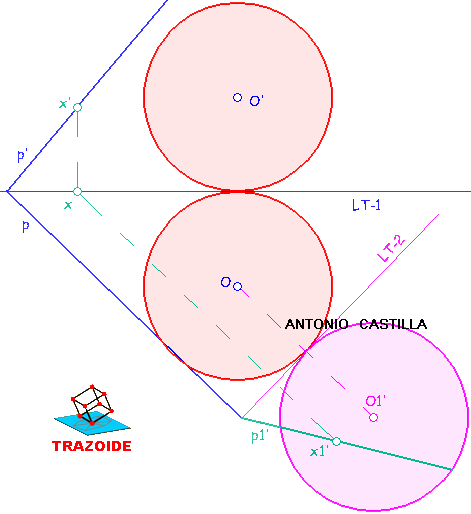
Cambiar de plano la esfera. Mediante una perpendicular a la segunda línea de tierra y llevando la cota del centro, O', se obtiene el centro de la esfera en el cambio de plano, O1'. Con el mismo radio de la esfera (en verdadera magnitud) se dibuja la esfera cambiada.
3 -
Cambiar el plano. Tomar un punto cualquiera, X, que tenga sus proyecciones sobre la traza vertical del plano, p', y en la línea de tierra. Trazar una perpendicular a la segunda línea de tierra, LT-2, por su proyección horizontal, x, y llevar la medida de la cota de la proyección vertical, obteniendo el punto cambiado, x1'. Unir con donde corta la traza horizontal del plano, p, a la segunda línea de tierra, LT-2, y este es el plano cambiado (proyectante), p1'.
4 -
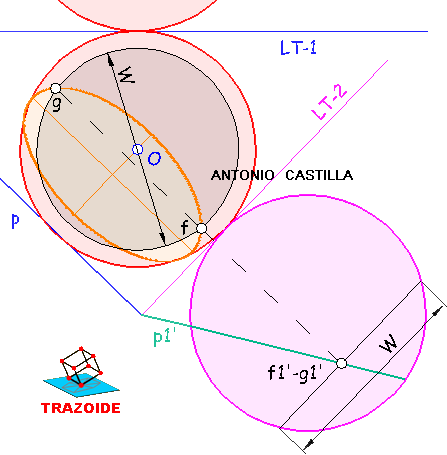
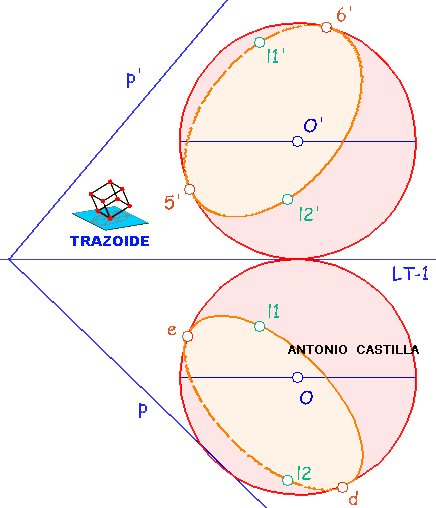
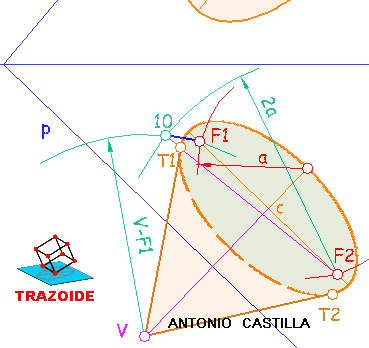
Eje menor de la elipse en proyección horizontal (ver la siguiente imagen). Llevar los puntos donde el plano en el cambio de plano, p1', toca a la esfera, a1' y b1', mediante perpendiculares a la segunda línea de tierra, hasta una perpendicular a la traza horizontal del plano, p, que pase por el centro de la esfera, O. Las nuevas proyecciones, a y b, son el eje menor de la elipse de la proyección horizontal.
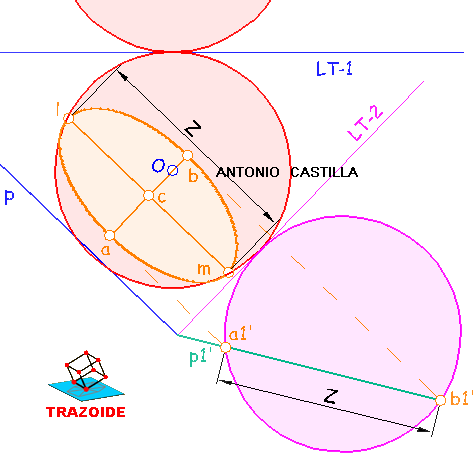
5 -
Eje mayor de la elipse en proyección horizontal. Tomar la medida, Z, en el cambio de plano, que hay entre los puntos de corte de la esfera con el plano, a1'-b1'. Llevar esta medida a una paralela a la traza horizontal del plano, p, que pase por el punto medio, c, del eje menor de la elipse,a-b (cuidado, NO es por el centro de la esfera). Este segmento, l-m, es el eje mayor de la elipse.
6 -
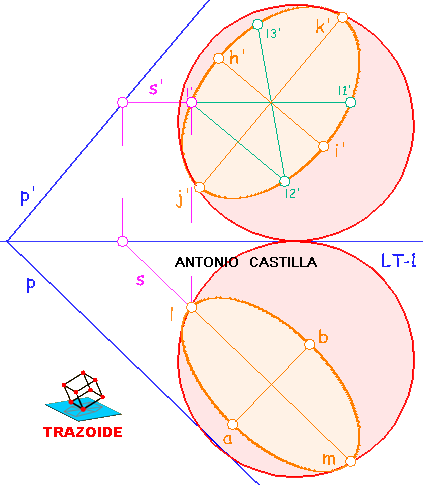
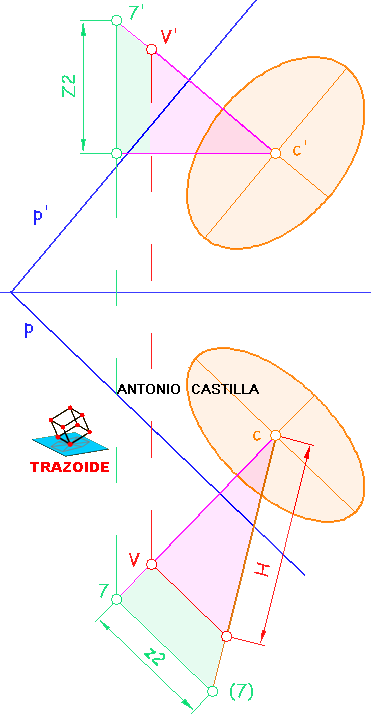
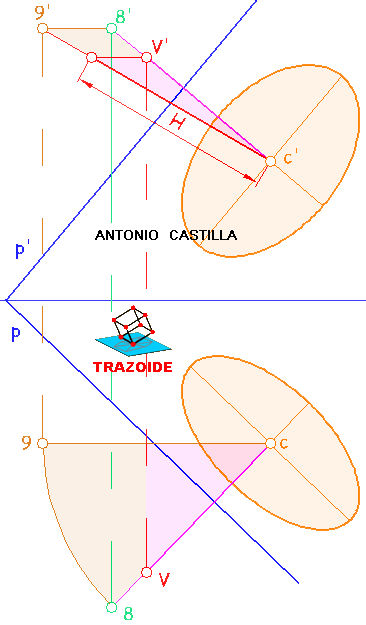
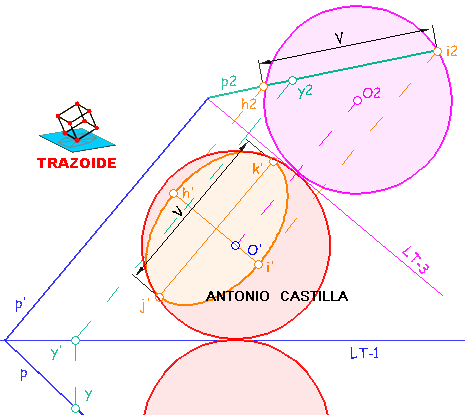
Ejes en la proyección vertical (ver la siguiente imagen). Se sigue el mismo proceso, pero con la tercera línea de tierra, LT-3, perpendicular a la traza vertical del plano, p'. El eje menor es H-I y el mayor J-K. Los puntos de los ejes en ambas proyecciones NO son los mismos, por lo que no hay correspondencia entre ellos. Si se halla la otra proyección de cada punto lo que se obtiene es un punto de la elipse, pero no los ejes.

 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí) El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado