Los puntos A'(8;12) B'(15,5;9,5) y C'(12,7;16) referidos al sistema de ejes cordenados definidos por los bordes de la lamina y origen el vertice inferior izqierdo, representan la perspectiva conica de un triangulo equilatero cuyo ortocentro es la proyección del centro del triangulo, se pide:
1. Determinad los elementos que definen la perspectiva cónica, sabiendo que la linea de tierra contiene al punto A'
2. Representar la perspectiva cónica de la piramide regular que tiene por base el triangulo indicado y por altura una magnitud igual al lado de la base.
3. Representar la sombra propia y arrojada sobre el plano horizontal, con luz paralela que forma 60º con el plano geometral y 30 con el plano del cuadro.
Gracias de antemano.
Problema piramide en conica
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
-
xtu_devilkam
- USUARIO

- Mensajes: 0
- Registrado: Jue, 11 Mar 2010, 23:36
- fernandore
- MODERADOR++

- Mensajes: 2094
- Registrado: Mar, 03 Jun 2008, 22:27
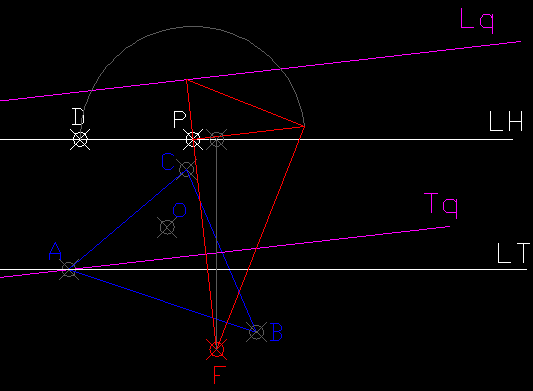
Primero tenemos q definir la homologia q transforma el triangulo dado en un triangulo equilatero.
1-Tenemos el triangulo ABC y hallamos los puntos 123 q son los pies de las alturas del triangulo dado y se corresponden con los puntos medios de los lados del triangulo equilatero q proporciona dicha perpectiva.
2-El triangulo 123 tambien debe ser equilatero y ademas los lados 13 y BC son paralelos.Por lo tanto se cortaran en la recta limite Lq.
3-Tambien son paralelos los lados 23 y AC,por lo tanto tambien se cortaran en la Lq.Con lo q la recta limite queda definida.
4-Por el punto A,trazamos una paralela a Lq y obtenemos el eje de homologia.Esto es asi porq el punto A pertenece al plano de cuadro al estar contenido en la LT.
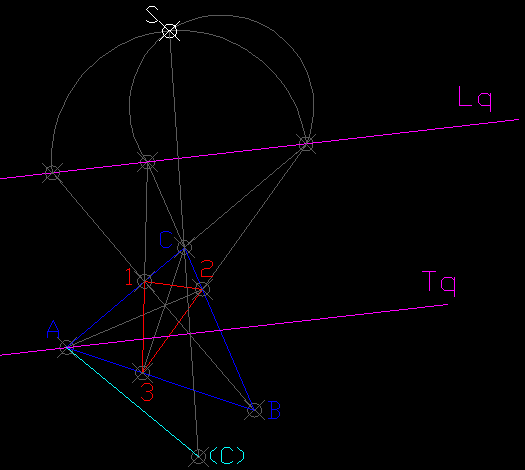
5-Para hallar el centro S de la homologia:
Trazamos el arco capaz de 60º sobre la Lq entre los puntos de corte con las prolongaciones de los lados AC y BC.
Trazamos el arco capaz de 90º entre los puntos de corte con las prolongacioes de los segmentos AC y B1.
Donde se cortan ambos arcos capaces obtenemos el centro de homologia.
6-Definida la homologia podemos hallar el triangulo equilatero (solo he hallado el punto C para mayor claridad en el dibujo ya q se superponen ambos triangulos)) q tiene por perpectiva conica el triangulo dado.
El triangulo equilatero dibujado se corresponde al abatimiento sobre el plano de cuadro del triangulo en cuestion.
El eje de homologia es la traza del plano del triangulo con el plano del cuadro y la recta limite es la recta de fugas o recta limite de dicho plano.
El centro de homologia se corresponde con el abatimiento sobre el cuadro del punto de vista,utilizando la Lq como charnela.
continuará...
- fernandore
- MODERADOR++

- Mensajes: 2094
- Registrado: Mar, 03 Jun 2008, 22:27
Ahora se trata de desabatir el centro de homologia tomando como charnela la recta Lq.
Para q el sistema conico esté definido hace falta q nos den la distancia principal (distancia del punto de vista al plano de cuadro).Este dato falta en el enunciado,yo he tomado PD=45mm.
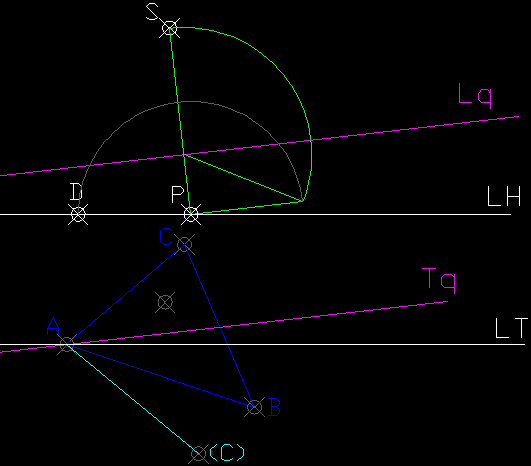
Una vez situado el punto P ya podemos trazar la LH y la LT.
Para q el sistema conico esté definido hace falta q nos den la distancia principal (distancia del punto de vista al plano de cuadro).Este dato falta en el enunciado,yo he tomado PD=45mm.

Una vez situado el punto P ya podemos trazar la LH y la LT.
- fernandore
- MODERADOR++

- Mensajes: 2094
- Registrado: Mar, 03 Jun 2008, 22:27
- fernandore
- MODERADOR++

- Mensajes: 2094
- Registrado: Mar, 03 Jun 2008, 22:27
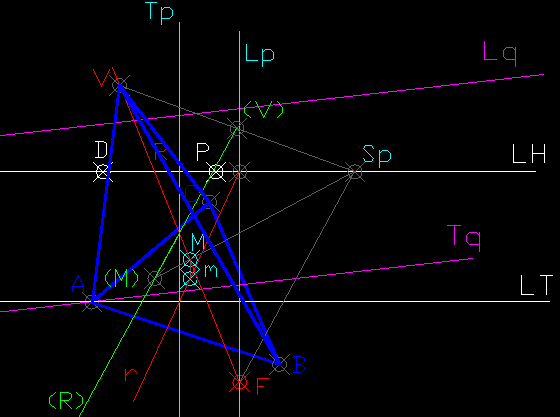
Para situar el vertice V de la piramide:
1-Tenemos q hallar la proyeccion secundaria del punto M (centro del triangulo).Para eso trazamos una recta cualquiera q pase por M y pertenezca al plano Q.(No esta dibujada)
2-Trazamos la recta R,recta perpendicular al plano del triangulo y q pasa por M.
3-Trazamos un plano P q contenga a la recta R.Yo he tomado un plano perpendicular al plano del cuadro (en cian)
4-Abatimos el plano P y la recta R (homologia de centro Sp,eje Tp y recta limite Lp).
5-Llevamos la distancia de la altura en el abatimiento.(Hay dos soluciones,si llevamos la distancia apartir de M hacia un lado o hacia el otro).
Situamos V en el abatimiento y desabatimos.
Salu2
- fernandore
- MODERADOR++

- Mensajes: 2094
- Registrado: Mar, 03 Jun 2008, 22:27
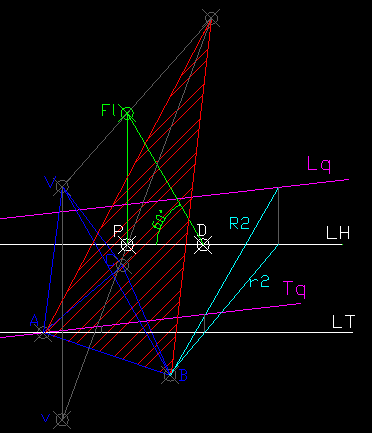
-Para realizar la sombra pedida en el enunciado primero tendremos q hallar el punto de fuga de los rayos luminosos.Sabemos q debe formar 60º con el geometral y 30º con el cuadro.Como la suma de ambos angulos es 90º solo cabe la posibilidad de q los rayos luminosos sean rectas de perfil.
Basta con contruir un triangulo rectangulo con uno de los catetos la distancia PD,para situar el punto de fuga Fl (en verde)
-Si trazamos por B una recta cualquiera contenida en el plano Q(plano de la base de la piramide) se puede comprobar q el punto B pertenece al plano geometral (ver recta R2 en cian)
-Trazamos la recta q pasa por V y por Fl y hallamos su traza con el geometral (punto donde se cortan las dos proyecciones,la directa y la horizontal) para situar su sombra.
-Como A y B estan en el geometral queda completada la sombra(la sombra de C queda interior)
Salu2
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 0 invitados