Homología de triángulo dificil
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
-
arsanchez90
- USUARIO

- Mensajes: 4
- Registrado: Vie, 20 Jun 2008, 01:35
Homología de triángulo dificil
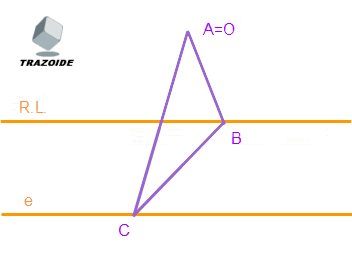
Dibujar triángulo homólogo de ABC; conociendo centro, eje (discontinua) y Recta límite


La figura origen es un triángulo. Uno de sus vértices, el A, que coincide con el centro de la homología (punto propio colineal a cualquier par de puntos homólogos). Otro, el C, que se encuentra en el eje de la homología, por lo que es doble (C=C´). Y el B, situado en RL; su homólogo es impropio, e.d., está en el infinito.
RESOLUCIÓN:
1. A es invariable, puesto que es el centro de la homología.
2. Une V con B, obteniendo la dirección de B´ en el infinito.
3. El lado AC corta a RL en X. La dirección de X´ en el infinito se halla uniendo VX. Estas direcciones las llevas sobre C´y sobre A´=A=V.
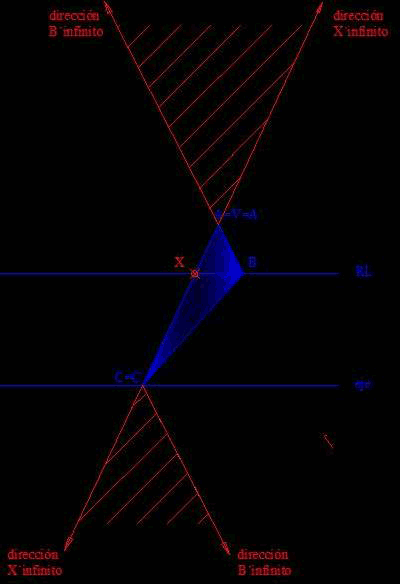
RESOLUCIÓN:
1. A es invariable, puesto que es el centro de la homología.
2. Une V con B, obteniendo la dirección de B´ en el infinito.
3. El lado AC corta a RL en X. La dirección de X´ en el infinito se halla uniendo VX. Estas direcciones las llevas sobre C´y sobre A´=A=V.

"Ahora puedo decirte que tomé la decisión correcta, sin embargo no hay un día que pase sin arrepentirme de no haber tomado una opción diferente".
Triangulo homologo ABC
Un dato no es el correcto te adjunto la fotografia del correcto, si hay algo que no esta claró pideme que lo especifique mejor.
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
-
carlosspanish
- USUARIO

- Mensajes: 0
- Registrado: Mar, 26 Nov 2013, 16:52
Homología de triángulo dificil
Hola Antonio. Querría saber cómo es posible que un triángulo tenga un vértice sobre el centro de homología, dado que éste está en un plano diferente al que contiene el eje de homología, donde está uno de los otros dos vértices. Gracias.
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
Recurriré a una imagen que hice hace algunos años y que tal vez no sea la mejor, pero así ahorro tiempo.
Explico primero lo que hay en la imagen.
Tenemos dos planos en el espacio, en azul y naranja, que contienen a la figura inicial, en este caso la recta R, y a la figura homológica, R', respectivamente.
La recta de intersección de ambos planos es el eje de la homología espacial, donde está E=E' (en mayúsculas).
El centro de la homología espacial es O, que como indicas es exterior a ambos planos.
Con estos elementos si desde el centro de homología lanzamos un rayo de proyección que pase por un punto D su homologo es D'.
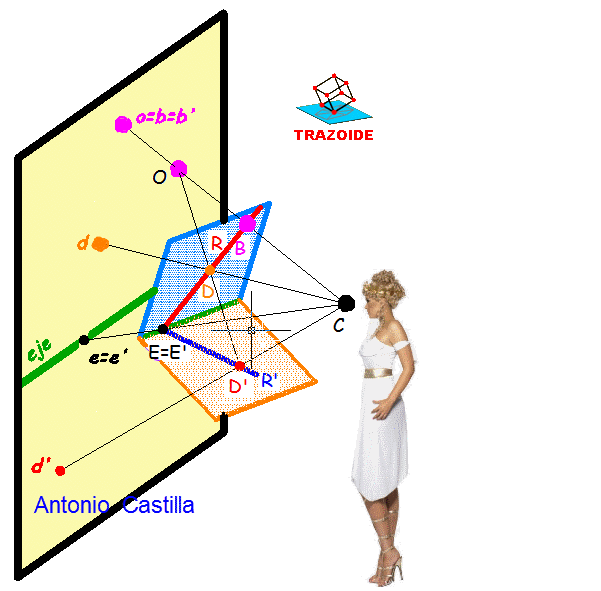
Pero todo esto es en el espacio y nosotros trabajamos en un plano (el papel o la pantalla del ordenador). Luego ahora situamos al observador dentro de la escena (la señorita, que aunque no soy yo me parezco mucho, ). Por comodidad reduciremos al observador a un punto C que será el centro de la proyección, no confundirlo con el centro de la homología.
). Por comodidad reduciremos al observador a un punto C que será el centro de la proyección, no confundirlo con el centro de la homología.
Situamos nuestro plano de proyección (el papel o la pantalla) detrás, en amarillo, y desde el centro de proyección C proyectamos todo. El centro de homología se proyecta en o (minúscula), el eje de la homología espacial se proyecta en el eje que marco con la palabra "eje", y los puntos de la homología espacial D y D' se proyectan en d y d'.
Una vez que entendemos lo que hay en la imagen vamos a tu duda. Supón un punto B sobre uno de los planos y que da la casualidad de que está en el rayo de proyección que sale del centro de proyección C y pasa por el centro de la homología espacial O. Al proyectar dicho punto B "caerá" en el plano de proyección sobre el centro de homología o y sin embargo eso no significa que estén uno sobre el otro en el espacio, simplemente es que están uno detrás del otro pero en el plano hemos perdido esa profundidad y da la falsa impresión de que son el mismo punto.
Recurriré a una imagen que hice hace algunos años y que tal vez no sea la mejor, pero así ahorro tiempo.
Explico primero lo que hay en la imagen.
Tenemos dos planos en el espacio, en azul y naranja, que contienen a la figura inicial, en este caso la recta R, y a la figura homológica, R', respectivamente.
La recta de intersección de ambos planos es el eje de la homología espacial, donde está E=E' (en mayúsculas).
El centro de la homología espacial es O, que como indicas es exterior a ambos planos.
Con estos elementos si desde el centro de homología lanzamos un rayo de proyección que pase por un punto D su homologo es D'.

Pero todo esto es en el espacio y nosotros trabajamos en un plano (el papel o la pantalla del ordenador). Luego ahora situamos al observador dentro de la escena (la señorita, que aunque no soy yo me parezco mucho,
Situamos nuestro plano de proyección (el papel o la pantalla) detrás, en amarillo, y desde el centro de proyección C proyectamos todo. El centro de homología se proyecta en o (minúscula), el eje de la homología espacial se proyecta en el eje que marco con la palabra "eje", y los puntos de la homología espacial D y D' se proyectan en d y d'.
Una vez que entendemos lo que hay en la imagen vamos a tu duda. Supón un punto B sobre uno de los planos y que da la casualidad de que está en el rayo de proyección que sale del centro de proyección C y pasa por el centro de la homología espacial O. Al proyectar dicho punto B "caerá" en el plano de proyección sobre el centro de homología o y sin embargo eso no significa que estén uno sobre el otro en el espacio, simplemente es que están uno detrás del otro pero en el plano hemos perdido esa profundidad y da la falsa impresión de que son el mismo punto.
-
carlosspanish
- USUARIO

- Mensajes: 0
- Registrado: Mar, 26 Nov 2013, 16:52
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 43 invitados


