Hola a todos.
El problema dice asi:
Un plano P (me lo dan) contiene la seccion principal de un tetraedro en la que los puntos m y n ( me dan estos dos puntos) son los extemos de la minima distancia de este tetraedro. Hallar las proyecciones del tetraedro.
Desgraciadamente no tengo escaner asi que no puedo poner el dibujo.
Se hace abatiendo el plano P y hallando alli los puntos m y n abatidos. Pero a apartir de alli ya no puedo hallar el lado de esa seccion principal.
no se si está claro..
Se que se obtiene por proporcionalidad pero no logro entender que proporcionalidad debo tener en cuenta.
Agradezco que me den algun consejo..Gracias.
Fernando
Minima distancia de un tetraedro
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
- fer_torres
- USUARIO

- Mensajes: 5
- Registrado: Vie, 15 Ago 2008, 17:46
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
La mínima distancia de la que te habla el problema es la distancia entre dos aristas opuestas.
En un tetraedro regular la mínima distancia entre sus aristas ( d.a ) es el segmento perpendicular a dos aristas opuestas, y va del punto medio de una arista hasta el punto medio de la opuesta.
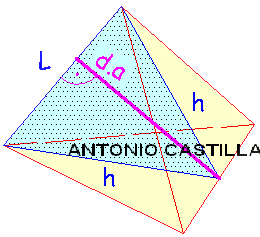
Esta distancia entre aristas está en la sección principal, perpendicular al lado de la sección principal que está formado con la medida del lado del tetraedro.
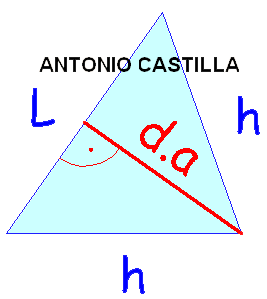
Para hallar el resto de las magnitudes conocida la distancia entre aristas ( d.a ), primero se elige un valor cualquiera para el lado ( L' ), con él se dibuja un triángulo equilátero y se determina su altura de cara ( h' ).
Conseguida la altura de cara se dibuja la sección principal con los valores de ese lado ( L' ) y la altura hallada ( h' ), el triángulo relleno de rosa en el dibujo siguiente.
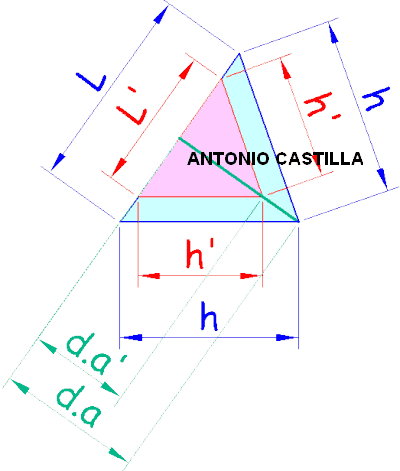
En ese triángulo se marca su distancia entre aristas ( d.a' ).
Sobre es distancia entre aristas ( d.a' ) se mide la distancia entre aristas que nos dan ( d.a ).
A partir de ese extremo se hacen paralelas a los lados de la sección principal. Con esto se obtiene un triángulo semejante (el relleno de celeste) en el que las magnitudes son equivalentes a las del otro, por lo que la que está sobre L' es L (lado buscado) y la que es paralela a h' es h (altura de cara buscada).
El resto del problema es como has comentado (con un abatimiento).
Respecto de las imágenes, no hace falta tener un escaner, os recuerdo que muchos tenéis teléfonos móviles con cámaras de fotos, o cámaras de fotos digitales o webcam, que pueden realizar una foto rápidamente aunque no se vea muy bien es mejor que nada.
La mínima distancia de la que te habla el problema es la distancia entre dos aristas opuestas.
En un tetraedro regular la mínima distancia entre sus aristas ( d.a ) es el segmento perpendicular a dos aristas opuestas, y va del punto medio de una arista hasta el punto medio de la opuesta.

Esta distancia entre aristas está en la sección principal, perpendicular al lado de la sección principal que está formado con la medida del lado del tetraedro.

Para hallar el resto de las magnitudes conocida la distancia entre aristas ( d.a ), primero se elige un valor cualquiera para el lado ( L' ), con él se dibuja un triángulo equilátero y se determina su altura de cara ( h' ).
Conseguida la altura de cara se dibuja la sección principal con los valores de ese lado ( L' ) y la altura hallada ( h' ), el triángulo relleno de rosa en el dibujo siguiente.

En ese triángulo se marca su distancia entre aristas ( d.a' ).
Sobre es distancia entre aristas ( d.a' ) se mide la distancia entre aristas que nos dan ( d.a ).
A partir de ese extremo se hacen paralelas a los lados de la sección principal. Con esto se obtiene un triángulo semejante (el relleno de celeste) en el que las magnitudes son equivalentes a las del otro, por lo que la que está sobre L' es L (lado buscado) y la que es paralela a h' es h (altura de cara buscada).
El resto del problema es como has comentado (con un abatimiento).
Respecto de las imágenes, no hace falta tener un escaner, os recuerdo que muchos tenéis teléfonos móviles con cámaras de fotos, o cámaras de fotos digitales o webcam, que pueden realizar una foto rápidamente aunque no se vea muy bien es mejor que nada.
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 17 invitados

