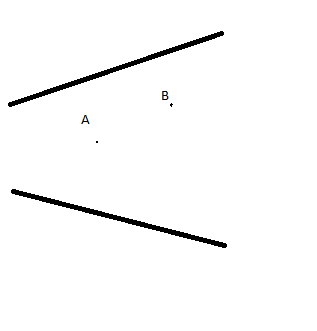
-Circunferencias tangentes a dos rectas secantes cuyo punto de corte es inaccesible y que pasen por el punto A y B, es decir, una circunferencia es tangente a las dos rectas y pasa por A y otra es tangente a las dos circunferencias y pasa por B.
Lo único que se de momento es que con la misma distancia en cada recta tengo que buscar el punto de corte y hacer la bisectriz y en esa recta se encontrarán los dos centros de las circunferencias, pero no se como encontrar el sitio exacto a no ser que sea a tanteo :mrgreen:
Gracias de antemano :)

 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado

