Puntos de intersección de una recta con una elipse
Gracias
Elipse: puntos de intersección con una recta t
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
-
PuturrúdeFuá
- USUARIO

- Mensajes: 145
- Registrado: Mar, 03 Jun 2008, 22:31
Puntos de intersección de una recta con una elipse
Tenemos los ejes de la elipse AB -mayor-, CD -menor- y la recta t
1º.- Se traza con centro en F y radio AB el arco focal
2º.- Se traza el punto F´1 simétrico del F´respecto de la recta t
Ahora hay que hallar las circunferencias tangentes al arco focal y que pasen por los puntos F´y F´1 para ello:
3º.- Se traza una circunferencia cualquiera que pase por los puntos F´y F´1 y cuyo centro esté en la recta t, cortando al arco focal en los puntos P1 y P2.
4º.-Las rectas P1P2 y F´F´1 se cortan en el centro radical Cr
5º.- Trazar por Cr las tangentes al arco focal, obteniendo los puntos de tangencia t1 y t2.
6º.- Las rectas t1F y t2F cortan a la recta en los puntos I1 e I2 que son los puntos de intersección buscados.
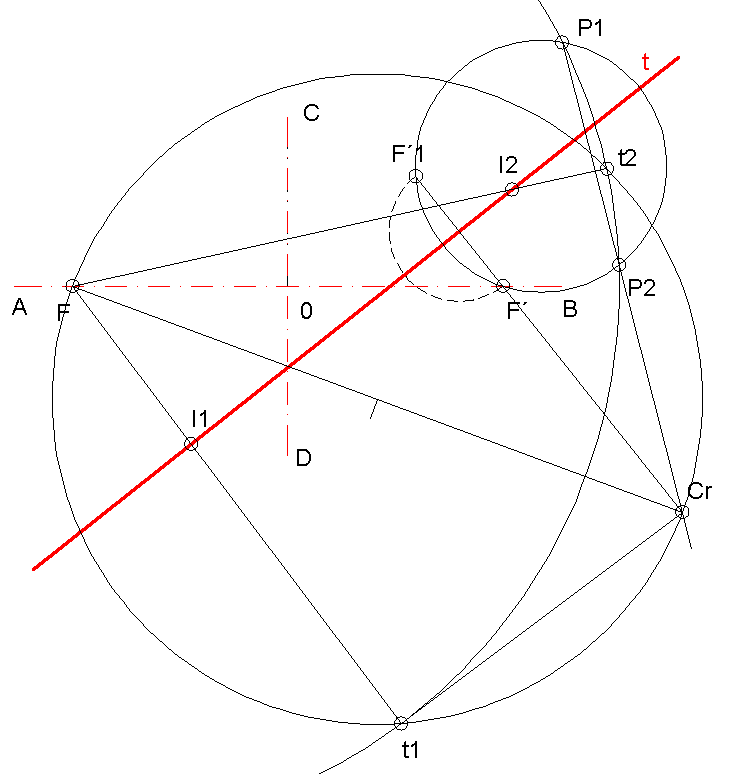
Tenemos los ejes de la elipse AB -mayor-, CD -menor- y la recta t
1º.- Se traza con centro en F y radio AB el arco focal
2º.- Se traza el punto F´1 simétrico del F´respecto de la recta t
Ahora hay que hallar las circunferencias tangentes al arco focal y que pasen por los puntos F´y F´1 para ello:
3º.- Se traza una circunferencia cualquiera que pase por los puntos F´y F´1 y cuyo centro esté en la recta t, cortando al arco focal en los puntos P1 y P2.
4º.-Las rectas P1P2 y F´F´1 se cortan en el centro radical Cr
5º.- Trazar por Cr las tangentes al arco focal, obteniendo los puntos de tangencia t1 y t2.
6º.- Las rectas t1F y t2F cortan a la recta en los puntos I1 e I2 que son los puntos de intersección buscados.

Estaba intentando realizar este problema. Mirando en diferentes fuentes de información, como internet o algunos libros de dibujo técnico que tengo, no era capaz de realizarlo. Pues todas las fuentes donde miro, me hablan de trazados muy complicados.
y mirando acá caí en la cuenta de:
creo que el problema se reduce a el problema de Apolonio circunferencia punto punto. (que es el mismo que recta punto punto)
la circunferencia la focal (la que se desee) y el simetrico del otro foco respecto a la recta.
A partir de ahí nos basamos en la resolucón del problema de tangencia compleja. (mediante potencia)
un saludo y gracias. Muy interesante este ejercicio. supongo que para parábolo e hipérbola es igual.
y mirando acá caí en la cuenta de:
creo que el problema se reduce a el problema de Apolonio circunferencia punto punto. (que es el mismo que recta punto punto)
la circunferencia la focal (la que se desee) y el simetrico del otro foco respecto a la recta.
A partir de ahí nos basamos en la resolucón del problema de tangencia compleja. (mediante potencia)
un saludo y gracias. Muy interesante este ejercicio. supongo que para parábolo e hipérbola es igual.
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 39 invitados

