1-Dado dos puntos (E y D) hallar los conjugados armonicos de razon dada a/b
Primero recordemos q 4 puntos alineados (EDNM) son conjugados armonicos si se verifica q
EM/MD=EN/DN
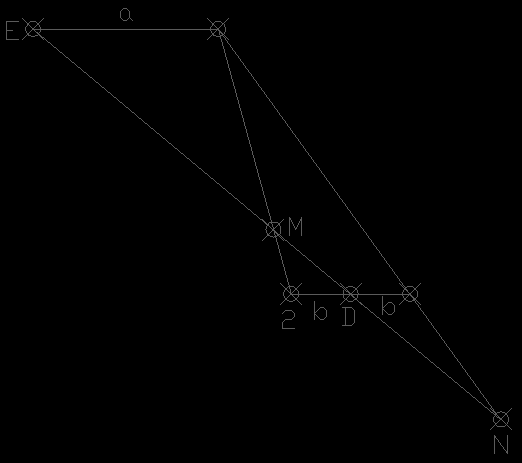
Si tenemos los puntos E y D y queremos situar 2 puntos M y N q sean conjugados armonicos,abrá infinitos pares de puntos,pero si ademas de q sean conjugados armonicos queremos q su razon sea a/b solo abrá un par de puntos q lo cumplan.
Efectivamente,si procedemos como en la figura adjunta podemos verificar aplicando proporcionalidad q EM/MD=EN/DN=a/b
2-Lugar geometico de los puntos cuyas distancias a otros 2 puntos fijos(E,D) estan segun una razon dada a/b
Existe una propiedad (q no voy a demostrar) q dice q dado dos puntos fijos E y D,el lugar geometico de puntos B cuya razon de distancias a E y D es constante,es una circunferencia.Es decir q los puntos B q verifican q BE/BD=a/b, estan sobre una circunferencia.
Ademas se verifica q los puntos diametrales de esa circunferencia son conjugados armonicos de razon a/b de los puntos fijos E y D.
Es decir q los puntos M y N seran el diametro de la circunferencia-lugar geometrico de los puntos B cuya razon de distancia a E y D es a/b.
RESOLUCION
Supongamos resuelto el problema.
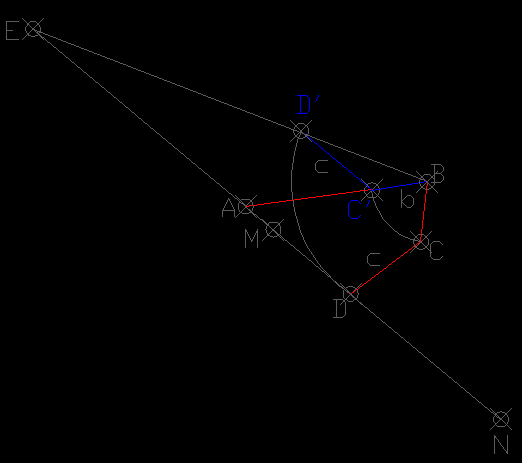
si pinchamos en el punto B y giramos los puntos C y D hasta situarlos segun la figursa en C' y D'.Observamos q el lado BD' es paralelo a la recta AD debido a q los angulos en C y en A son suplementarios ya q el cuadrilatero es inscriptible.
Unimos el punto B con el D' y situamos el punto E.
Por proporcionalidad se verifica q AE/D'C'=AB/C'B o lo q es lo mismo AE/c=a/b Luefo el punto E se puede situar hallando la cuarta proporcional de a,b,c
Por otro lado la razon de distancia de B a E y D será BE/BD=BE/BD' q aplicando proporcionalidad BE/BD'=a/b
Luego B pertenece al lugar geometrico cuya razon de distancia a E y D es a/b.
Ese lugar geometrico es la circunferencia de diametro MN,donde M y N son los conjugados armonicos de razon a/b de los puntos E y D.
Es decir q trazando la circunferencia de diametro MN podemos situar el punto B ya q la distancia AB=a nos es conocida.
Una vez situado el punto B los demos puntos son inmediatos.
Salu2

 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado






