triangulo sobre tres rectas paralelas *
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
- martacumbre
- USUARIO

- Mensajes: 8
- Registrado: Vie, 13 Jun 2008, 18:58
triangulo sobre tres rectas paralelas *
¿ Como se haria un triángulo equilátero que tenga cada uno de sus vértices apoyado en tres rectas paralelas ?
Muchas gracias, seguir así, sois el mejor foro que hay, o mas bien el único que merece la pena.
Muchas gracias, seguir así, sois el mejor foro que hay, o mas bien el único que merece la pena.
Un pequeño tropiezo puede impedir una gran caída (dicho inglés)
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
Triángulo equilátero que tenga cada uno de sus vértices apoyado en tres rectas paralelas, R, S y T
1 - Tomar un punto cualquiera en una de ellas, el punto A por ejemplo.
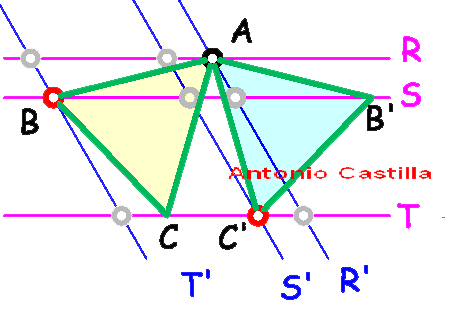
2 - Girar (da igual el sentido de giro) las tres rectas alrededor de ese primer vértice,
un ángulo igual 60º. Para ello :
4 - De los puntos marcados NO nos interesan aquellos que son puntos de corte de una
recta con su homónima girada, ni tampoco los que pertenecen a la recta que contenía al primer vértice ni el de su girada. Luego, solo son necesarios donde se intersecan las rectas iniciales con una de las giradas que no sea de su homónima.
6 - Si salen varios puntos, cada uno de ellos indica una solución distinta, y habrá tantas soluciones como puntos nos den.
7 - Unir el punto inicial con una de las soluciones y esa recta será el lado del polígono buscado. Dibujarlo a partir del lado.
Triángulo equilátero que tenga cada uno de sus vértices apoyado en tres rectas paralelas, R, S y T
1 - Tomar un punto cualquiera en una de ellas, el punto A por ejemplo.

2 - Girar (da igual el sentido de giro) las tres rectas alrededor de ese primer vértice,
un ángulo igual 60º. Para ello :
- Dibujar la recta R' formando 60º respecto de la recta R y pasando por el punto A.
- Hacer las rectas S' y T' paralelas a la recta R' separadas la misma distancia que había entre R y S.
4 - De los puntos marcados NO nos interesan aquellos que son puntos de corte de una
recta con su homónima girada, ni tampoco los que pertenecen a la recta que contenía al primer vértice ni el de su girada. Luego, solo son necesarios donde se intersecan las rectas iniciales con una de las giradas que no sea de su homónima.
6 - Si salen varios puntos, cada uno de ellos indica una solución distinta, y habrá tantas soluciones como puntos nos den.
7 - Unir el punto inicial con una de las soluciones y esa recta será el lado del polígono buscado. Dibujarlo a partir del lado.
triangulo sobre tres rectas paralelas
Hola estoy haciendo este método y no me sale me lo podrías explicar mas a fondo, soy un poco torpe entendiendo las explicaciones.
Me encanta esta pagina, Felicidades!!
Gracias!!
Me encanta esta pagina, Felicidades!!
Gracias!!
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
Una vez giradas las rectas, debes ver donde se cortan unas con otras (en mi dibujo marcados con pequeños círculos grises y rojos).

Pero todos esos puntos no son válidos.
Debes descartar los puntos que estén sobre una recta y su girada, es decir, no valen los puntos donde S corta a S', ni donde T corta a T'.
Tampoco son validos los puntos que están sobre la recta en la que está el punto que se tomó inicialmente, A, es decir, no son válidos los puntos que están sobre R o R'.
Una vez descartados esos puntos los que nos queden (los puntos de corte de S con T' y de T con S') son las distintas soluciones.
Una vez giradas las rectas, debes ver donde se cortan unas con otras (en mi dibujo marcados con pequeños círculos grises y rojos).

Pero todos esos puntos no son válidos.
Debes descartar los puntos que estén sobre una recta y su girada, es decir, no valen los puntos donde S corta a S', ni donde T corta a T'.
Tampoco son validos los puntos que están sobre la recta en la que está el punto que se tomó inicialmente, A, es decir, no son válidos los puntos que están sobre R o R'.
Una vez descartados esos puntos los que nos queden (los puntos de corte de S con T' y de T con S') son las distintas soluciones.
Rotación
El punto A está en la recta r (podría estar en la s o en la t), si consideramos hacer un triángulo ABC en sentido horario, entonces el punto C es la imagen de una rotación de B de -60º con centro en A.
Hacemos una rotación de la recta s que contiene a B, y obtenemos s'. El punto en que se interceptan s' y t es el punto C, que es la imagen de un punto de s (B), por lo que pertenece a s'. Tenemos el lado AC, y encontramos el punto B al construir un triángulo equilátero en dirección de la recta s.
Hacemos una rotación de la recta s que contiene a B, y obtenemos s'. El punto en que se interceptan s' y t es el punto C, que es la imagen de un punto de s (B), por lo que pertenece a s'. Tenemos el lado AC, y encontramos el punto B al construir un triángulo equilátero en dirección de la recta s.
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
Hola.
Tengo apuntes de éste ejercicio o parecidos y es una pena que se queden en mi ordenador.
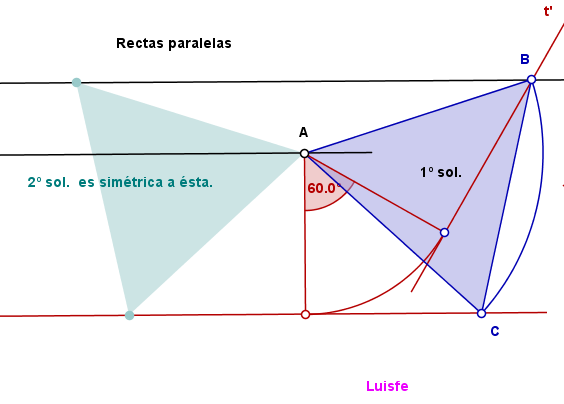
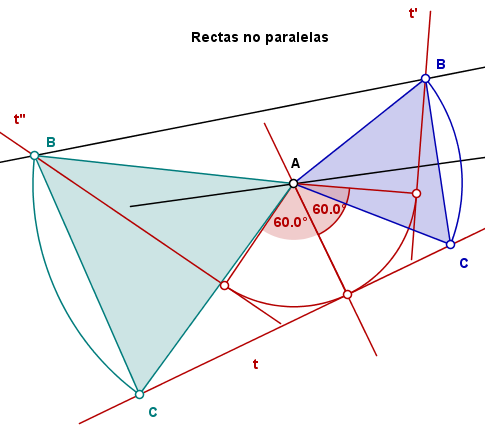
Una forma "diferente" de mirar éste ejercicio pero que en realidad es lo mismo, sería como muestro en el dibujo.
El punto lo he situado en la 2º recta, pero da igual donde esté, la cosa NO CAMBIA NADA.
Gira 60º (por que es un triángulo equilátero) una de las rectas en las que no esté el punto de partida.
el punto de corte de la girada con la 3º recta será un vértice solución.
No importa que las rectas iniciales estén paralelas o no, es el mismo procedimiento.
Saludos
Tengo apuntes de éste ejercicio o parecidos y es una pena que se queden en mi ordenador.
Una forma "diferente" de mirar éste ejercicio pero que en realidad es lo mismo, sería como muestro en el dibujo.
El punto lo he situado en la 2º recta, pero da igual donde esté, la cosa NO CAMBIA NADA.
Gira 60º (por que es un triángulo equilátero) una de las rectas en las que no esté el punto de partida.
el punto de corte de la girada con la 3º recta será un vértice solución.
No importa que las rectas iniciales estén paralelas o no, es el mismo procedimiento.
Saludos


¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 23 invitados


