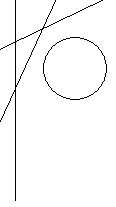Ejercicios sobre elipses, hipérbolas y parábolas.
-
robertbn1
- USUARIO

- Mensajes: 9
- Registrado: Sab, 30 Ago 2008, 08:11
Mensaje sin leer
por robertbn1 » Mié, 01 Oct 2008, 16:28
Hola, necesito saber
como se hace el ejercicio del que te dan tres tangentes a la parabola y la circunferencia donde se encuentra el foco y te piden hallar la parabola.
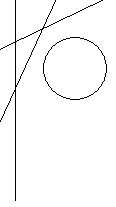
Un saludo
-
Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
Mensaje sin leer
por Antonio Castilla » Mié, 01 Oct 2008, 16:34
.
La cosa sería así :
1 - Hacer la simétrica de la circunferencia respecto de cada una de las tangentes.
2 - Eso da tres nuevas circunferencias, que se deberán de cortar entre sí (sin la posición exacta no te lo puedo asegurar)
3 - Une los puntos de corte de las tres circunferencias simétricas y tienes la recta directriz de la parábola
4 - Halla el simétrico del punto de corte de dos de las circunferencias simétricas respecto de las tangentes y ese será el foco de la parábola
5 - El eje es perpendicular a la recta directriz y pasando por el foco
6 - A partir de ahí, traza la parábola
-
sergio_14192
- USUARIO

- Mensajes: 0
- Registrado: Mié, 08 Dic 2010, 23:13
Mensaje sin leer
por sergio_14192 » Jue, 09 Dic 2010, 18:26
Definir una parábola, conociendo tres tangentes y el lugar geométrico del foco.
Para resolver este problema, antes tenemos que definir el TEOREMA DE LAMBERT que nos sirve para resolver este problema de parábola.
El TEOREMA DE LAMBERT nos dice que la circunferencia circunscrita al triángulo que definen tres tangentes a una parábola pasa por el foco de la misma.
Luego lo que tenemos que hacer es lo siguiente:
1. Hallamos las mediatrices del tríangulo que forman las tangentes y tenemos el centro de la circunferencia circunscrita.
2. Construimos la circunferencia circunscrita y donde corte al lugar geométrico del foco, es decir, la circunferencia dato, obtenemos el FOCO.
3. Para hallar la directriz sabemos a través del TEOREMA DE STEINER que el ortocentro del tríanfulo que definen las tres tangentes a una parábola pertenece a su directriz. Luego obtenemos la directriz.
Todas estas propiedades se deducen del teorema de SIMPSON.
Un saludo espero que os sirva de mucha ayuda.
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 26 invitados
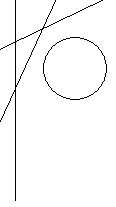
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí) El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado