Sé que la solución del enunciado es la circunferencia de centro O' :) . No consigo demostrar ni por qué es esa circunferencia, ni por qué CB y MO son paralelas. Ayuda por favor!
LG de los puntos del plano que son el punto medio de las cuerdas, con un extremo fijo, de una circunferencia. *
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
LG de los puntos del plano que son el punto medio de las cuerdas, con un extremo fijo, de una circunferencia. *
LG de los puntos del plano que son el punto medio de las cuerdas, con un extremo fijo, de una circunferencia.
Sé que la solución del enunciado es la circunferencia de centro O' :) . No consigo demostrar ni por qué es esa circunferencia, ni por qué CB y MO son paralelas. Ayuda por favor!
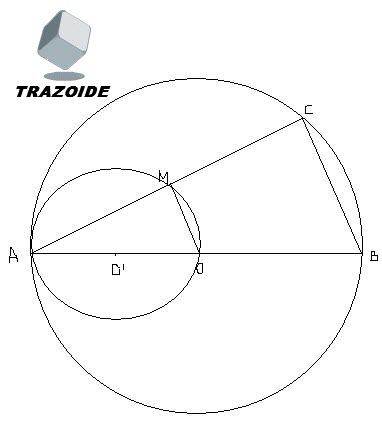
Sé que la solución del enunciado es la circunferencia de centro O' :) . No consigo demostrar ni por qué es esa circunferencia, ni por qué CB y MO son paralelas. Ayuda por favor!
Hola. No sé hasta que nivel de profundidad hay que demostrar el ejercicio.
De manera intuitiva se vé que si el extremo del segmento se pasea por la circunferencia (el otro fijo), su punto medio irá al compás de ése movimiento, creando tras de sí la misma línea de movimiento, es decir, otra circunferencia con valor la mitad ya que
se trata del punto medio.
El centro del LG de los puntos medios está en el punto medio del segmento que une el extremo A con el centro de la circunferencia.
Se entiende que el segmento más largo posible sería el mismo diámetro con su punto medio en O y el más pequeño el mismo punto A. Entre éstos dos puntos estaría el centro del LG.
También se puede hablar de que las dos circunferencias trazadas son homotéticas a razón 1/2 con el centro de homotécia
en A. Ésto hace que los triángulos formados en tu dibujo sean semejantes y por tanto se entiende ese paralelismo.
No sé, se podría profundizar más o verlo desde otros puntos, pero ahí lo dejo.
¿Qué ocurriría con una elipse?
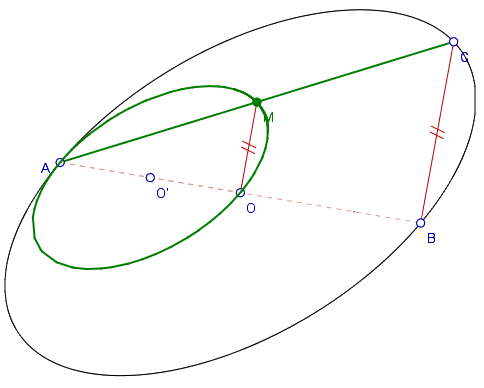
De manera intuitiva se vé que si el extremo del segmento se pasea por la circunferencia (el otro fijo), su punto medio irá al compás de ése movimiento, creando tras de sí la misma línea de movimiento, es decir, otra circunferencia con valor la mitad ya que
se trata del punto medio.
El centro del LG de los puntos medios está en el punto medio del segmento que une el extremo A con el centro de la circunferencia.
Se entiende que el segmento más largo posible sería el mismo diámetro con su punto medio en O y el más pequeño el mismo punto A. Entre éstos dos puntos estaría el centro del LG.
También se puede hablar de que las dos circunferencias trazadas son homotéticas a razón 1/2 con el centro de homotécia
en A. Ésto hace que los triángulos formados en tu dibujo sean semejantes y por tanto se entiende ese paralelismo.
No sé, se podría profundizar más o verlo desde otros puntos, pero ahí lo dejo.
¿Qué ocurriría con una elipse?

¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 27 invitados



