En una afinidad de eje dada, Transforma el triangulo escaleno ABC en uno equilátero con la condición en la cual el triangulo transformando este por debajo del eje.
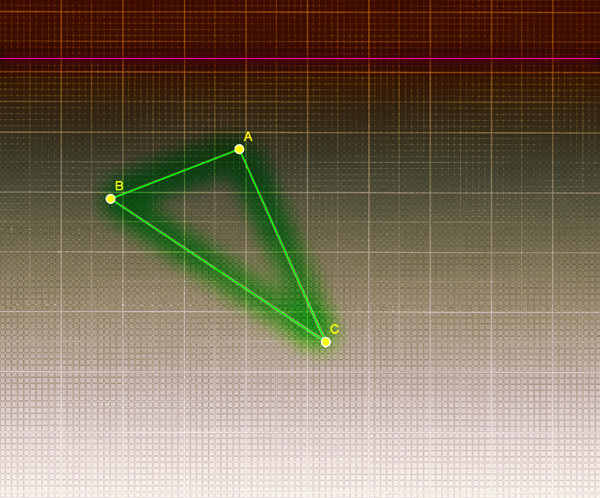
SOLUCIÓN:
1 – Prolongamos el lado A-C y A-B hasta cortar al eje en los puntos 1 y 2.
2 – Hacer un arco capaz de 60º del segmento 1-2:
- a) Para ello trazamos la mediatriz del segmento 1-2 (perpendicular al eje desde punto 3).
- b) Dibujamos una semirrecta desde el punto 1 con el Angulo complementario de 60º (30º).
- c) El punto de intersección de la mediatriz y la semirrecta anteriormente dibujadas es el centro del arco capaz de 60º (punto E).
- d) Con centro en el punto E y radio E-1 dibujamos el arco capaz.
4 – Prolongamos A-D hasta cortar al eje en el punto 4.
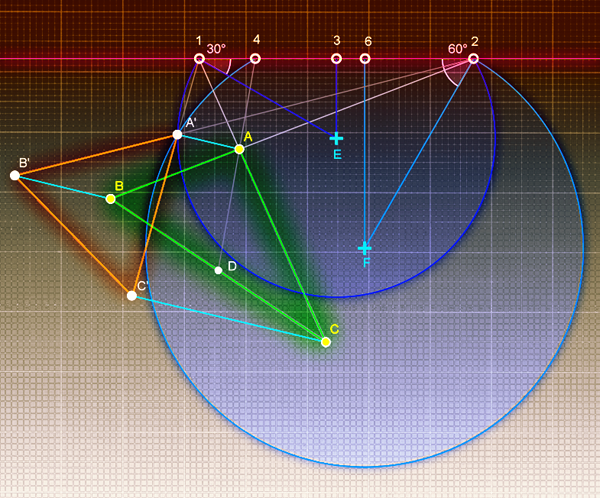
5 – Dibujamos un arco capaz de 30º del segmento 2-4:
- a) Para ello trazamos la mediatriz del segmento 2-4 (perpendicular al eje desde punto 6).
- b) Dibujamos una semirrecta desde el punto 2 con el Angulo complementario de 30º (60º).
- c) El punto de intersección de la mediatriz y la semirrecta anteriormente dibujadas es el centro del arco capaz de 30º (punto F).
- d) Con centro en el punto F y radio F-2 dibujamos el arco capaz.
7 – La intersección de la semirrecta 1-A’ y la paralela a A-A’ desde el punto C determina el punto afín C’.
8 – La intersección de la semirrecta 2-A’ y la paralela a A-A’ desde el punto B determina el punto afín B’.
9 – Con esto ya obtenemos el triangulo pedido que cumple la condición de ser equilátero y estar por debajo del eje de afinidad.

 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado




