.
Aparte de lo que te ha comentado Celedonio, te lo explico con autocad en 3d que creo que es como lo pides aunque no indicas nada.
1 - En el plano XY del SCP universal, construir un triángulo rectángulo ADC, con  = 30º, C = 60º y D = 90º. Las longitudes de los lados son indiferentes porque vamos a determinar la posición de los tirantes con los ángulos dados y después hallaremos su longitud. Aunque es mejor si la longitud de la hipotenusa AC es una cantidad fácil de recordar como por ejemplo 50.
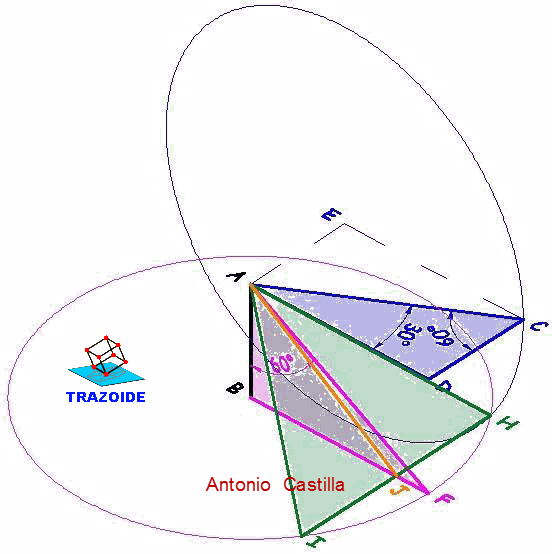
2 - Por el extremo C trazamos una paralela al cateto AD, esto nos da CE.
3 - Con centro en E y radio CE dibujamos una circunferencia. La circunferencia se gira 90º alrededor del eje CE.
4 - Gira el SCP alrededor del eje X un ángulo de 90º. Sobre la línea AD dibujar otra que mida lo mismo que la hipotenusa AC y girarla hasta que forme 60º con el eje Y, línea AF.
5 - Por A trazar una paralela al eje Y y por F otra paralela a X para formar un triángulo rectángulo, ABF.
6 - Volver el SCP a su posición universal y dibujar una circunferencia con centro en B y radio BF.
7 - Unir el punto de corte de ambas circunferencias, H, con el punto común de los dos triángulos, A. Esta AH es la dirección de uno de los tirantes.
8 - Por simetría dibujar el otro tirante, AI.
9 - Unir los extremos de los dos tirantes, H e I, y unir el punto medio J de HI con A. Esta última, AJ, es la dirección de la línea que unirá el centro de gravedad con el extremo del mástil.
10 - Conocidas todas las direcciones, se dibuja la pérgola, es decir un triángulo equilátero de 2'5 m de lado y se determina su centro de gravedad, G.
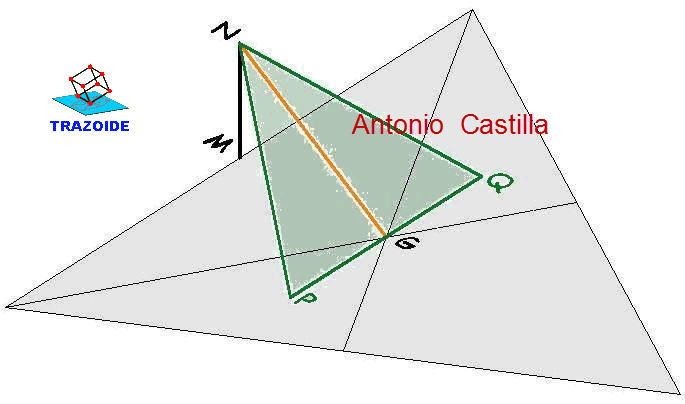
11 - Por el centro de gravedad, G, se dibuja una paralela a la dirección AJ, y por el punto medio, M, de uno de sus lados una paralela al eje Z. Prolongarlas hasta que se corten, punto N, y el segmento vertical MN es la parte del mástil que sobresale de la pergola.
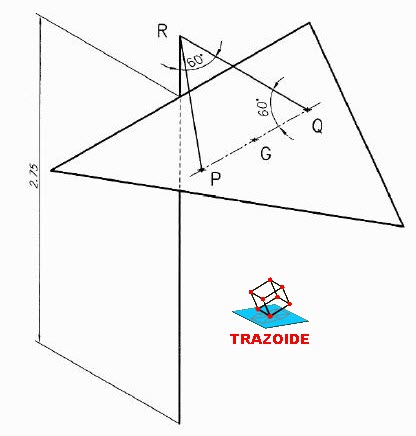
12 - Por el centro de gravedad, G, se dibuja una paralela al lado y por N paralelas a AH y AI. Prolongar las tres líneas hasta que se corten entre sí, formando el triángulo NPQ que son los tirantes y puntos de sujeción buscados.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado





