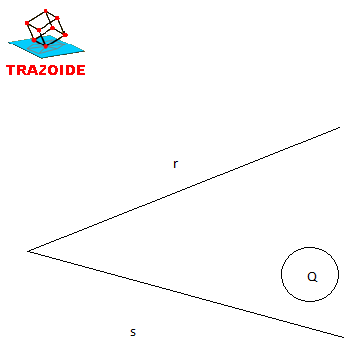
Circunferencias tangentes a la dada y a las rectas *
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
Circunferencias tangentes a la dada y a las rectas *
Wenas os dejo aquí el ejercicio, necesito hacerlo mediante homotecia


- fernandore
- MODERADOR++

- Mensajes: 2093
- Registrado: Mar, 03 Jun 2008, 22:27
1-Traza 2 rectas R' y S`paralelas a R y S a una distancia igual al radio de la circunferencia (puedes trazarla por fuera o por dentro,cada caso te dará 2 soluciones distintas)
2-Por homotecia traza la circunferencia q siendo tangente a R' y S' pasan por el centro de la circunferencia dada.
Aqui puedes ver como es el procedimiento viewtopic.php?f=5&t=2167&start=0
3-A la circunferencia anterior le sumas o restas(segun si R' y S' las has tomado exteriores o interiores) el radio de la cirncunferencia dada y obtienes la circunferencia solucion
Salu2
2-Por homotecia traza la circunferencia q siendo tangente a R' y S' pasan por el centro de la circunferencia dada.
Aqui puedes ver como es el procedimiento viewtopic.php?f=5&t=2167&start=0
3-A la circunferencia anterior le sumas o restas(segun si R' y S' las has tomado exteriores o interiores) el radio de la cirncunferencia dada y obtienes la circunferencia solucion
Salu2
-
Jose Maroto
- USUARIO

- Mensajes: 6
- Registrado: Sab, 14 Ene 2012, 16:31
Buenas .
Yo estoy buscando lo mismo con la condición de que la circunferencia solución forma 30º con una de las rectas, 45º con la otra y tangente a la circunferencia.
No consigo hallar con la solución. Hallo la recta en donde se encuentran los centros de todas las que forman esos ángulos con las rectas y nada más.
A ver si alguién me ayuda. Gracias.
Yo estoy buscando lo mismo con la condición de que la circunferencia solución forma 30º con una de las rectas, 45º con la otra y tangente a la circunferencia.
No consigo hallar con la solución. Hallo la recta en donde se encuentran los centros de todas las que forman esos ángulos con las rectas y nada más.
A ver si alguién me ayuda. Gracias.
Hola. Creo que lo pides por HOMOTECIA ¿no?. Si es así, en realidad es lo mismo que ya sabemos para el caso normal pero con algún matiz que hay tener en cuenta.
Si sabes como "calar" o cortar una circunferencia en una recta con un ángulo determinado, lo sabrás hacer en dos rectas.
Suponiendo que sí, esa es la circunferencia que tienes que llevar homoteticamente al lugar correcto.
Para convertir el caso RRC a RRP tienes que tener cuidado, al acercar las rectas en la dilatación porque se trasladan
(yo lo he hecho así) la distancia de la circunferencia dada sí, pero en ángulo (ver el dibujo).
Intuyo de todas maneras que hay otras formas (como siempre) de solucionar el ejercicio.
Saludos.
Si sabes como "calar" o cortar una circunferencia en una recta con un ángulo determinado, lo sabrás hacer en dos rectas.
Suponiendo que sí, esa es la circunferencia que tienes que llevar homoteticamente al lugar correcto.
Para convertir el caso RRC a RRP tienes que tener cuidado, al acercar las rectas en la dilatación porque se trasladan
(yo lo he hecho así) la distancia de la circunferencia dada sí, pero en ángulo (ver el dibujo).
Intuyo de todas maneras que hay otras formas (como siempre) de solucionar el ejercicio.
Saludos.
Última edición por luisfe el Lun, 10 Dic 2012, 19:11, editado 1 vez en total.
-
Jose Maroto
- USUARIO

- Mensajes: 6
- Registrado: Sab, 14 Ene 2012, 16:31
Si, creo que es un poco más corto. Al principio suelo pensar en aplicar Inversión con éste tipo de ejercicios, cuando hay que hallar circunferencias secantes con un ángulo concreto. Con un centro de inversión y valor más apropiado, hallaríamos las inversas de las 2 rectas, que serían 2 circunferencias de las cuales hay hallar como antes, el lugar geométrico de las rectas que lasJose Maroto escribió:Comenté por homotecia porque no se me ocurría otro camino más corto.
cortan en el ángulo pedido y en éstas procederíamos a hallar las tangentes interiores y exteriores a ambas. Luego las inversas de éstas, serían las soluciones (provisionales antes de revertir la dilatación)
Aún así, hay que tener cuidado al hacer las dilataciones, puesto que sigue valiendo lo que dije anteriormente de separar las rectas en ángulo (30º y 45º respecto de la perpendicular en el ejercicio planteado) y en el sentido correcto.
Saludos.
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 45 invitados


