3 problemas de hiperbolas
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
3 problemas de hiperbolas
Hola buenas tardes, ¿alguien me puede ayudar con alguno de estos tres ejercicios? supongo que tendra que ver con simetricos. muchas gracias de antemano.
1º - Construir una hiperbola conociendo un foco 2 puntos y la magnitud 2a.
2º - Construir una hiperbola conociendo dos focos y una tangente.
3º - Construir una hiperbola conociendo las asintotas(+-45º) y la magnitud b
1º - Construir una hiperbola conociendo un foco 2 puntos y la magnitud 2a.
2º - Construir una hiperbola conociendo dos focos y una tangente.
3º - Construir una hiperbola conociendo las asintotas(+-45º) y la magnitud b
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
Para el primero :
Hipérbola conocidos dos puntos, P y Q, un foco, F1, y el eje mayor, 2a
1 - Con centro en uno de los puntos, P, y radio la suma de la distancia entre ese punto y el foco, x, más 2a se hace un arco
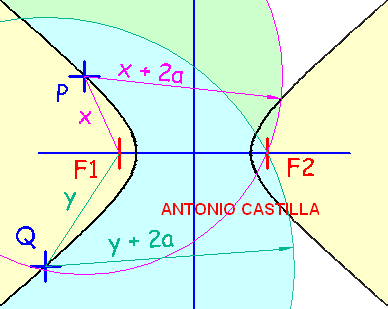
2 - Se repite con el otro punto, Q, siendo el radio y + 2a
3 - Donde se corten es el segundo foco
MÁS ABAJO ESTÁ RESUELTO DE NUEVO ESTE PROBLEMA
Para el primero :
Hipérbola conocidos dos puntos, P y Q, un foco, F1, y el eje mayor, 2a
1 - Con centro en uno de los puntos, P, y radio la suma de la distancia entre ese punto y el foco, x, más 2a se hace un arco

2 - Se repite con el otro punto, Q, siendo el radio y + 2a
3 - Donde se corten es el segundo foco
MÁS ABAJO ESTÁ RESUELTO DE NUEVO ESTE PROBLEMA
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
Para el segundo :
Hipérbola conocidos los dos focos y una tangente
a - Se halla el simétrico, s1, de uno de los focos respecto de la tangente
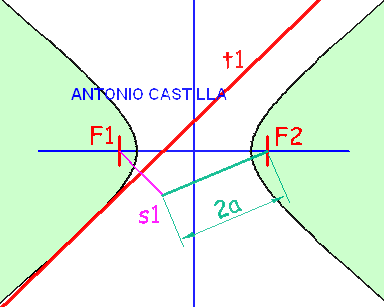
b - Al unir el simétrico, s1, con el otro foco se obtiene la medida del eje mayor, 2a
c - Uniendo los dos focos se tiene la distancia focal
d - Desde el centro de este último se lleva la medida del eje mayor, 2a, para determinar los vértices de la hipérbola
Para el segundo :
Hipérbola conocidos los dos focos y una tangente
a - Se halla el simétrico, s1, de uno de los focos respecto de la tangente

b - Al unir el simétrico, s1, con el otro foco se obtiene la medida del eje mayor, 2a
c - Uniendo los dos focos se tiene la distancia focal
d - Desde el centro de este último se lleva la medida del eje mayor, 2a, para determinar los vértices de la hipérbola
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
Para el tercero :
Hipérbola conociendo las asintotas(+-45º) y la magnitud b
I - Por el ángulo de las asíntotas se trata de una hipérbola equilátera
II - En ese caso el valor del semieje mayor es igual al de semieje menor, a = b
III - Dibujar los dos ejes perpendiculares entre si
IV - Hacer las asíntotas formando 45º con los ejes
V - Sobre el eje mayor colocar su valor y levantar una perpendicular hasta la asíntota
VI - Con esto se forma un triángulo en el que la hipotenusa es el valor de la semidistancia focal
Para el tercero :
Hipérbola conociendo las asintotas(+-45º) y la magnitud b
I - Por el ángulo de las asíntotas se trata de una hipérbola equilátera
II - En ese caso el valor del semieje mayor es igual al de semieje menor, a = b
III - Dibujar los dos ejes perpendiculares entre si
IV - Hacer las asíntotas formando 45º con los ejes
V - Sobre el eje mayor colocar su valor y levantar una perpendicular hasta la asíntota
VI - Con esto se forma un triángulo en el que la hipotenusa es el valor de la semidistancia focal
Triangulo en una hiperbola
Este es dificil:
3. El triangulo de vertices P, Q y F es tal que F representa un foco de una hiperbola, siendo P y Q dos puntos de la curva. Sabiendo que el eje real de la cónica mide 3cm, hallar el otro foco y los ejes de simetría de la cónica así definida, en la solución con mayor distancia focal. Datos: PF= 6 cm, QF= 5 cm, PQ= 4 cm.
Muchas gracias!!
3. El triangulo de vertices P, Q y F es tal que F representa un foco de una hiperbola, siendo P y Q dos puntos de la curva. Sabiendo que el eje real de la cónica mide 3cm, hallar el otro foco y los ejes de simetría de la cónica así definida, en la solución con mayor distancia focal. Datos: PF= 6 cm, QF= 5 cm, PQ= 4 cm.
Muchas gracias!!
Hola.
Sale un hipérbola bastante feucha , espero que esté bien :mrgreen: .
, espero que esté bien :mrgreen: .
Situa los puntos FPQ.
F2 está en el cruce de dos distancias:
Desde P esta a PF+2a y desde Q está a QF+2a
(se podría restar también la , distancia al foco - 2a pero dará menor distancia entre focos (aunque más bonita la curva, jeje))
Sólo tienes que trazar ambos arcos y donde se crucen (2 lugares)
tienes F2.
Lo demás es sencillo.
Ya por hoy lo dejo . ah! un consejo muy bueno, MIRA EN LOS ÍNDICES, encontrarás de todo, bueno, bonito y barato
Saludos.
MÁS ARRIBA ESTÁ RESUELTO DE NUEVO ESTE PROBLEMA
Sale un hipérbola bastante feucha
Situa los puntos FPQ.
F2 está en el cruce de dos distancias:
Desde P esta a PF+2a y desde Q está a QF+2a
(se podría restar también la , distancia al foco - 2a pero dará menor distancia entre focos (aunque más bonita la curva, jeje))
Sólo tienes que trazar ambos arcos y donde se crucen (2 lugares)
tienes F2.
Lo demás es sencillo.
Ya por hoy lo dejo . ah! un consejo muy bueno, MIRA EN LOS ÍNDICES, encontrarás de todo, bueno, bonito y barato
Saludos.
MÁS ARRIBA ESTÁ RESUELTO DE NUEVO ESTE PROBLEMA
Última edición por luisfe el Lun, 14 Ene 2013, 13:00, editado 2 veces en total.
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 13 invitados


