homologia de una circunferencia parábola *
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
homologia de una circunferencia parábola *
Hola me piden la homologia de una circunferencia-parábola. Pero con la especialidad que el centro de homologia esta sobre el eje, y el centro de la circunferencia también. las medidas que me dan son eje x=120, RL x=70, Ch(120,190), centro circunferencia (120,140), r=50. a ver si alguien me puede echar una mano. gracias
hola. Espero haber tomado bien los datos.
Este es un tema que lo tengo un poco "oxidado" pero haciendo un esfuercillo te diré:
La homología de la circunferencia al ser tangente a la recta límite fuerza a que la homologa sea una parábola.
La construcción que yo he realizado es la siguiente.
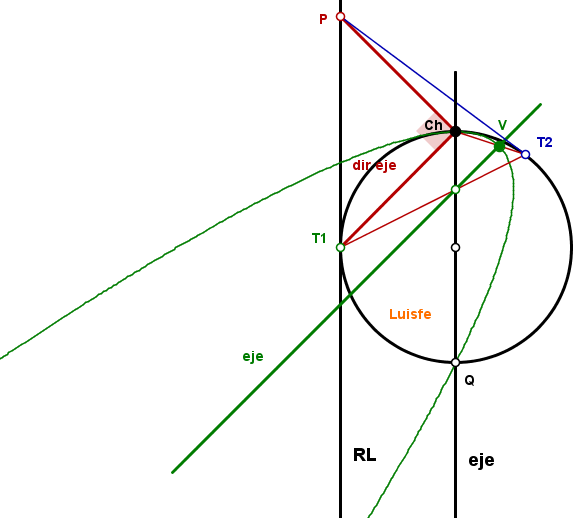
1. Segmento dir eje. Une el punto de tangencia T1 (RL-circunferencia) con el Centro Ch.
2. Perpendicular a dir eje hasta cortar a la RL en P.
3.Hallar T2, punto tangente desde P a la circunferencia.
4.Recta s . Une los dos puntos de tangencia T1 y T2 y donde corta al eje será el punto E.
5.Eje de la parábola. Paralela a dir eje por E
6.Vértice. Une Ch con T2 y donde corta al EJE tienes V. (V es homólogo del punto de tangencia T2)
Con el EJE y el Vértice y Ch como punto de la parábola puedes construir la cónica
por el procedimiento normal. Para ello tendrías que hallar su parámetro. lo tienes en los índices.
O bien pudes por homologia crear todos los puntos que quieras.
Por cierto al otro lado de Ch diametralmente tienes también otro punto de la parábola (Q) lógicamente .
Espero que te ayude.
Dibujito.
 Saludos
Saludos
homología circunferencia parábola
Aunque también debido a la configuración de los datos en éste caso podemos abreviar de la siguiente manera:
el eje de la parábola es la mediatriz de la cuerda focal ChM'. M' es el punto medio entre Ch y M.
Las tangentes en Ch (el centro Ch es además un punto doble) y M' son perpendiculares y paralelas respectivamente al eje de homología.
Este es un tema que lo tengo un poco "oxidado" pero haciendo un esfuercillo te diré:
La homología de la circunferencia al ser tangente a la recta límite fuerza a que la homologa sea una parábola.
La construcción que yo he realizado es la siguiente.
1. Segmento dir eje. Une el punto de tangencia T1 (RL-circunferencia) con el Centro Ch.
2. Perpendicular a dir eje hasta cortar a la RL en P.
3.Hallar T2, punto tangente desde P a la circunferencia.
4.Recta s . Une los dos puntos de tangencia T1 y T2 y donde corta al eje será el punto E.
5.Eje de la parábola. Paralela a dir eje por E
6.Vértice. Une Ch con T2 y donde corta al EJE tienes V. (V es homólogo del punto de tangencia T2)
Con el EJE y el Vértice y Ch como punto de la parábola puedes construir la cónica
por el procedimiento normal. Para ello tendrías que hallar su parámetro. lo tienes en los índices.
O bien pudes por homologia crear todos los puntos que quieras.
Por cierto al otro lado de Ch diametralmente tienes también otro punto de la parábola (Q) lógicamente .
Espero que te ayude.
Dibujito.
 Saludos
Saludoshomología circunferencia parábola
Aunque también debido a la configuración de los datos en éste caso podemos abreviar de la siguiente manera:
el eje de la parábola es la mediatriz de la cuerda focal ChM'. M' es el punto medio entre Ch y M.
Las tangentes en Ch (el centro Ch es además un punto doble) y M' son perpendiculares y paralelas respectivamente al eje de homología.
muchísimas gracias, estaba atascado, soy estudiante de uclm en Toledo y tenemos un profesor como te diría yo... vamos no tenemos apuntes, ni nos los da en clase, solo hace laminas, y sencillas, encima se une q como dibujo es una asignatura opcional de entrada yo no he dado nunca dibujo.... de nuevo muchas gracias..
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 26 invitados



