Hola. Es difícil saber el nivel de quién pregunta (...y del que contesta,

)
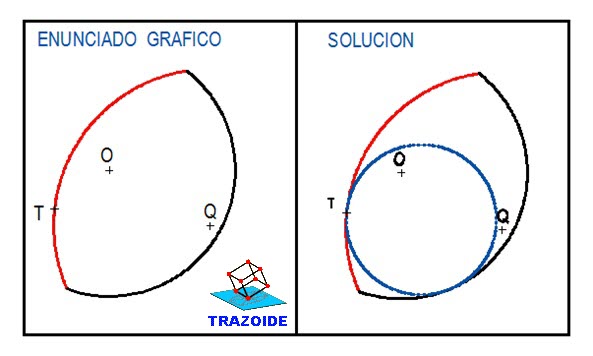
por eso, a veces con sólo ver el dibujo vamos tirando. Si estás comenzando te explico:
Une el punto de tangencia que te dan (T) con el centro del arco Q.
En esa recta tendrá que estar el centro solución. ¿Pero dónde exactamente? :roll: .
Hay que tener en cuenta lo siguiente:
El Centro radical CR es un punto en el que las tangentes desde él a los arcos y a la solución que queremos buscar, son de la misma longitud (igual POTENCIA). Si encontramos éste punto CR sabremos hallar donde se encuentra el otro punto de tangencia T2 en el otro arco.
Por otro lado, todas las circunferencias con centro en la recta que une a TQ y son tangentes
en T, tienen el mismo CR. y éste se encuentra en la perpendicular a TQ por T ,pero, ¿en qué punto de esa perpendicular ? :-? pues si trazamos una circunferencia auxiliar cualquiera con centro en la recta TQ tangente a T y que corte además al arco de O , la recta que pase por éstos puntos de corte nos llevará a CR igualmente.
Por lo tanto la perpendicular y ésta última recta se cortan en CR, guay! 8-) .
Teniendo en cuenta la propiedad mencionada anteriomente de CR , El punto de tangencia desde CR a el arco de O (negro)
es equidistante y obtendremos T2 inmediatamente. Ya sólo queda unir T2 con O y donde corta a TQ estará el centro solución.

Estúdialo un poquito y veras que es mas sencillo de lo que parece

.
Ciao.
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí) El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado