Bueno... ¡Todavía estoy esperando los JAMONES!

Hoy hago así estos ejercicios. De hecho los debo de tener en alguna parte de mi ordenador o quizás los haya posteado ya.
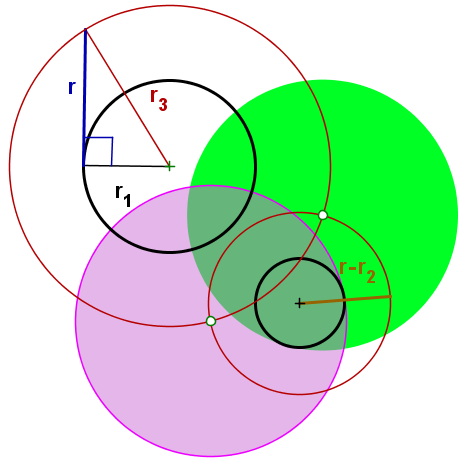
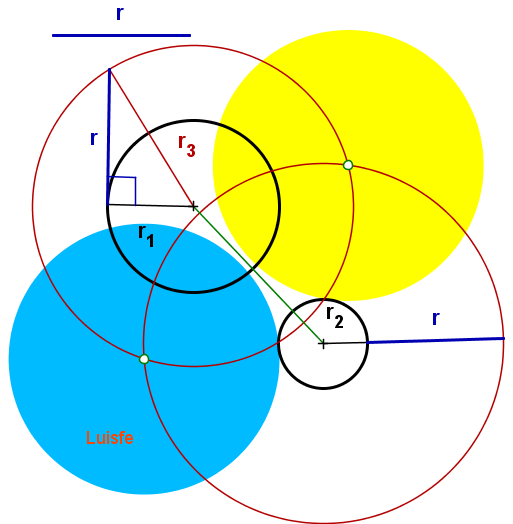
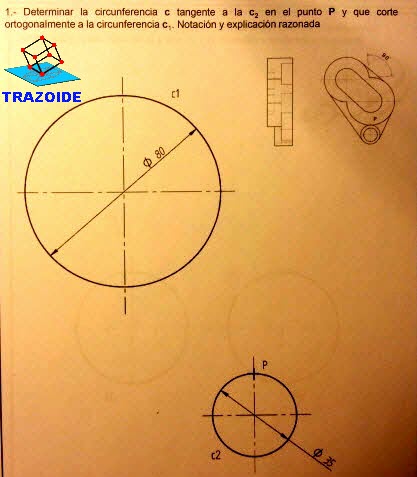
Sólo te paso los dibujos
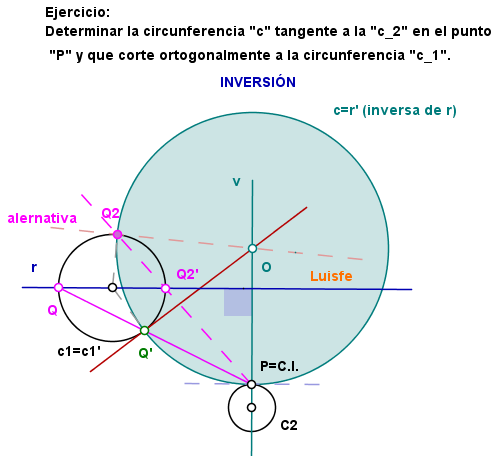
El 1º procedimiento es por INVERSIÓN .
Las explicaciones de ésta "curiosa" construcción podrían parecer un cuento de hadas, puntos
en el infinito, rectas que vienen del más allá, dependiendo de algunas consideraciones, me explico:
En ésta misma inversión con P como centro de ella, se pueden consideran uno elementos u otros,
es decir, puede entrar en juego la inversa de c2, o bien, olvidarnos de ella y
sustituirla por una recta perpendicular a PO2 por el punto P ("horizontal"), o bien, sustituirla por
la recta de centros soluciones (v) que sabemos que es la recta que pasa por PO2 (la "vertical" v),
pero en todos los casos, nos quedamos siempre con c1' (=c1).
Quizás la más fácil de entender sea la última opción, en la que tendríamos
como inversas a c1' y la de la recta de centros v' , de tal manera que si hacemos pasar una recta
(r en el dibujo) perpendicular a c1' y a v', su inversa (la circunferencia solución) tendrá un comportamiento idéntico respecto de c1 y v.
Ya sé que es mucho rollo :roll: , pero son datos que pueden ser útiles una vez que se madura la idea.
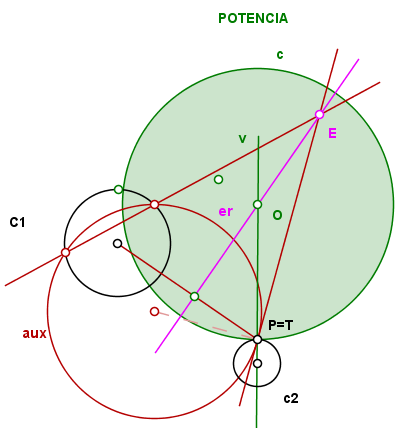
El 2º procedimiento es por POTENCIA.
Es hallar el eje radical de c1 y el punto P el cual cortará a la "vertical" en el centro buscado.
¡Suerte!
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí) El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado