Mensaje sin leer
por luisfe » Mar, 28 May 2013, 12:17
Hola.
Yo no empleo la circunferencia de puntos dobles cpd para resolver ésta tangencia, pero si quieres calcularla no tienes más
que saber que los puntos, por ejemplo, A' A señalados en el dibujo (hay más) son inversos y se hace lo mismo con ellos que lo que se hace con C3,C3'.
Para éste caso, con ese centro directo I+ de inversión positiva puedes calcular 2 soluciones, pero sabrás que puedes utilizar un centro de inversión negativa I- también, de modo que te salen otras dos soluciones más, pero ésto es un poco salirnos de la pregunta que planteas.
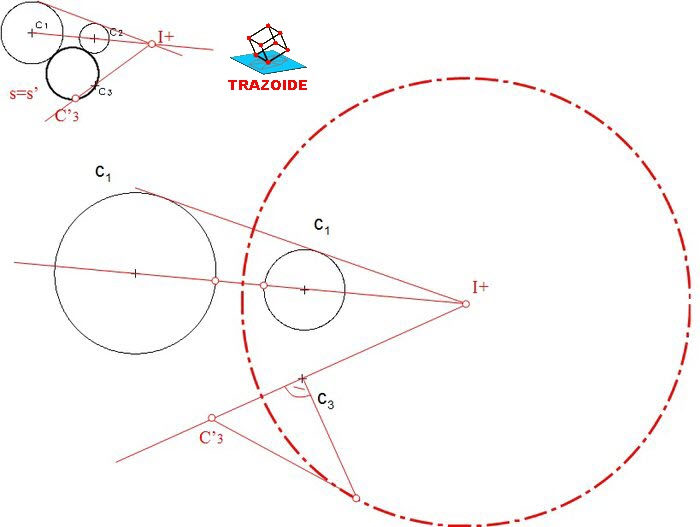
Para el caso que nos ocupa, para calcular C3' , lo corriente es hacer pasar una circunferencia por una pareja de inversos conocidos, en éste caso A' A y el punto C3, luego igual que aquí, conectaríamos C3 con I+ y donde corta su prolongación a la circunferencia tenemos C3'.
Hay que saber que 2 parejas de puntos inversos son cíclicos, es decir, se puede hacer pasar una circunferencia por ellos.
la circunferencia solución S=S' significa que es una circunferencia doble; un punto X de ella tiene su inverso X' en ella misma, como pasa también con C3 y C3', habiendo además 2 puntos dobles que son los puntos de corte con la cpd.
Una vez hallado C3' te queda una tangencia CPP que la puedes terminar de varias maneras, quizás lo más cómodo sea terminarla por POTENCIA.
Sobre éste tema he posteado en otras ocasiones pero ahora no sé exactamente dónde. Espero que en algo te ayude.
Saludos.
-
Adjuntos
-

- Tangente_a_dos_circunferencias_y_que_pase_por_un_punto_dado-10b.png (39.88 KiB) Visto 179 veces

 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado



