recta paralela
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
recta paralela
Muy buenas amigos, tengo un problemilla que me gustaría que me ayudaseis a resolver: el asunto es el que sigue.
Dadas dos rectas(A y B) que se cruzan se pide hallar un segmento paralelo a un plano dado de tal forma que se apoye en A y en B.
Los datos :
La recta A que pasa por M(50,110.0) y N(140,20,80)
La recta B que pasa por O(40,0,40) y P(140,60,10)
El plano alfa que pasa por Q(0,0,0) R(20,30,0) y S(40,0,60)
Por tanto el problema queda:
Encontrar un punto" X "de la recta A y otro "Y" de la recta B con la condición de que "XY" sea paralelo al plano alfa.
Muchas gracias.
Dadas dos rectas(A y B) que se cruzan se pide hallar un segmento paralelo a un plano dado de tal forma que se apoye en A y en B.
Los datos :
La recta A que pasa por M(50,110.0) y N(140,20,80)
La recta B que pasa por O(40,0,40) y P(140,60,10)
El plano alfa que pasa por Q(0,0,0) R(20,30,0) y S(40,0,60)
Por tanto el problema queda:
Encontrar un punto" X "de la recta A y otro "Y" de la recta B con la condición de que "XY" sea paralelo al plano alfa.
Muchas gracias.
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
Te comento el procedimiento :
1 - Hacer un cambio de plano de todo con la segunda línea de tierra perpendicular a la traza horizontal del plano (en azul)
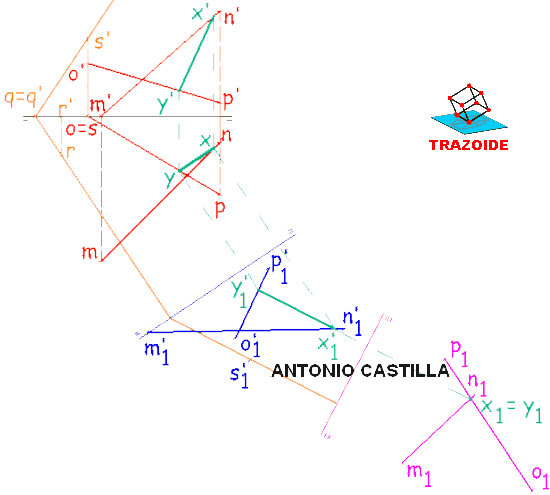
2 - Volver a hacer otro cambio de plano de todo con la tercera línea de tierra perpendicular a la traza del plano cambiada (en magenta)
3 - En el último cambio de plano el punto de corte de las dos proyecciones de las rectas es la recta buscada x1y1
4 - Deshacer los cambios de planos mediante perpendiculares a las líneas de tierra. La verdadera magnitud esta en el primer cambio de plano.
Te comento el procedimiento :
1 - Hacer un cambio de plano de todo con la segunda línea de tierra perpendicular a la traza horizontal del plano (en azul)

2 - Volver a hacer otro cambio de plano de todo con la tercera línea de tierra perpendicular a la traza del plano cambiada (en magenta)
3 - En el último cambio de plano el punto de corte de las dos proyecciones de las rectas es la recta buscada x1y1
4 - Deshacer los cambios de planos mediante perpendiculares a las líneas de tierra. La verdadera magnitud esta en el primer cambio de plano.
¿es posible resolver este problema de la siguiente manera?
1º Plano paralelo a al dado que contenga a un punto (p1) cualquiera de una de las rectas
2ºInterseccion de ese plano con una de la otra recta
3º Union de (p1) y la intersección obtenida
Adjunto el dibujo que me sale ( se me a movido un poco )
Gracias a todos¡¡
1º Plano paralelo a al dado que contenga a un punto (p1) cualquiera de una de las rectas
2ºInterseccion de ese plano con una de la otra recta
3º Union de (p1) y la intersección obtenida
Adjunto el dibujo que me sale ( se me a movido un poco )
Gracias a todos¡¡
- fernandore
- MODERADOR++

- Mensajes: 2093
- Registrado: Mar, 03 Jun 2008, 22:27
- fernandore
- MODERADOR++

- Mensajes: 2093
- Registrado: Mar, 03 Jun 2008, 22:27
- fernandore
- MODERADOR++

- Mensajes: 2093
- Registrado: Mar, 03 Jun 2008, 22:27
Gaudí hacía mucho uso del paraboloide hiperbólico para sus cúpulas y techos. El motivo es que esta estructura bidimensional es la mejor para resistir los esfuerzos internos de presión-tensión, por lo que de forma barata pueden obtenerse techados con gran resistencia de carga.
Ademas ,aunq las superficies alabeadas no son desarrollables,se pueden construir con relativa facilidad al ser superficies regladas.
Salu2
Ademas ,aunq las superficies alabeadas no son desarrollables,se pueden construir con relativa facilidad al ser superficies regladas.
Salu2
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 42 invitados

