Enlazar dos rectas con condiciones *
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
-
Jose Maroto
- USUARIO

- Mensajes: 6
- Registrado: Sab, 14 Ene 2012, 16:31
Enlazar dos rectas con condiciones *
Leyendo un problema de diédrico repasando el foro me acuerdo de un problema para el que no tengo solución. Lo escribí allí pero como realmente es de acotados también lo escribo en este lado. Si está mal hecho, lo siento. Lo borran y ya está.
Me dan 2 rectas, AB y CD y me piden: hallar dos segmentos diferentes de pendiente 2/1 que enlacen las dos rectas de tal forma que el punto de conexión en la recta CD sea, para uno de los casos el de mayor cota posible y para el otro el de menos cota posible.
Las dos rectas son oblicuas, se cruzan y la AB tiene mayor cota que la CD.
Gracias.
Me dan 2 rectas, AB y CD y me piden: hallar dos segmentos diferentes de pendiente 2/1 que enlacen las dos rectas de tal forma que el punto de conexión en la recta CD sea, para uno de los casos el de mayor cota posible y para el otro el de menos cota posible.
Las dos rectas son oblicuas, se cruzan y la AB tiene mayor cota que la CD.
Gracias.
-
Jose Maroto
- USUARIO

- Mensajes: 6
- Registrado: Sab, 14 Ene 2012, 16:31
Entiendo que requieran los datos para resolver problemas concretos, pero este es un planteamiento genérico. Entiendo que con las mismas instrucciones se resolverá igual independientemente de los datos.
De todas formas si se requieren unos puntos obligatoriamente se pueden inventar unos cualesquiera.
Gracias.
De todas formas si se requieren unos puntos obligatoriamente se pueden inventar unos cualesquiera.
Gracias.
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
Este ejercicio lo tenía resuelto hace muchos años pero por más que lo busco en el foro no aparece, es una de esas cosas que desaparece misteriosamente. Después de llevarme otro buen rato buscando entre mis archivos lo he encontrado. Te pongo primero el enunciado y a medida que vaya subiendo las imágenes lo voy colgando.
Enunciado :
Los segmentos AB y CD definen los ejes de dos galerías mineras que se quieren unir por otra galería que tenga un 2% de pendiente y cuyo extremo en la galería definida por CD tenga un desnivel de +2 m. respecto a su extremo en la galería definida por AB.
DATOS:
A(25; 180; 55) B(262.5; 257.5; 95) C(45, 45; 60) D(165; 377.5, 95) Cotas en metros. Escala 1/2500
Este ejercicio lo tenía resuelto hace muchos años pero por más que lo busco en el foro no aparece, es una de esas cosas que desaparece misteriosamente. Después de llevarme otro buen rato buscando entre mis archivos lo he encontrado. Te pongo primero el enunciado y a medida que vaya subiendo las imágenes lo voy colgando.
Enunciado :
Los segmentos AB y CD definen los ejes de dos galerías mineras que se quieren unir por otra galería que tenga un 2% de pendiente y cuyo extremo en la galería definida por CD tenga un desnivel de +2 m. respecto a su extremo en la galería definida por AB.
DATOS:
A(25; 180; 55) B(262.5; 257.5; 95) C(45, 45; 60) D(165; 377.5, 95) Cotas en metros. Escala 1/2500
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
Voy a dar una explicación de mi razonamiento. Los dibujos que ofrezco son esquemas, no es el dibujo real, ni están hechos con medidas.
El razonamiento y los esquemas que doy son en el espacio, no aplicando el sistema acotado.
RAZONAMIENTO :
Supongamos que sobre el plano horizontal tengo el punto A (ver el esquema debajo de este párrafo). A partir de él levanto una recta con una pendiente del 2% y localizo sobre ella el punto P, que está dos metros por encima del punto A. La proyección de esa recta, AP, es el cateto horizontal de 100 m de largo.
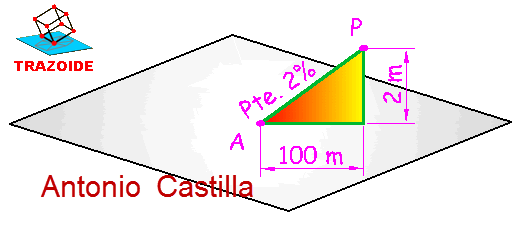
Ahora bien, existen infinitas posiciones para la recta AP, que se consiguen al girar el triángulo de la pendiente alrededor de A. Cualquiera de esos puntos sería una solución, luego todos los posibles puntos (lugar geométrico) que son solución forman una circunferencia de radio 100 m y centro 2 m por encima del punto A (la circunferencia magenta en el siguiente esquema).
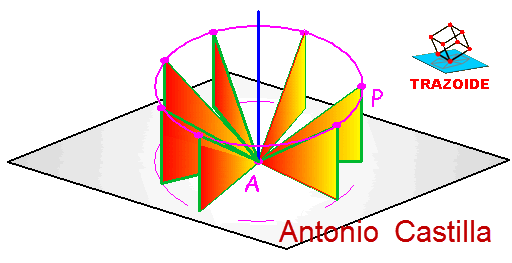
Pero, claro está, no va a dar la casualidad de que la recta que buscamos parta del punto A (dado en el enunciado), sino que saldrá de otro que esté sobre la recta AB. Es por eso que puedo aplicar idéntico razonamiento a todos los infinitos puntos entre A y B. Esto dará infinitas circunferencias donde estarán las posibles soluciones (perdonar que no haya dibujado las infinitas circunferencias y me haya conformado con solo tres en el esquema siguiente).
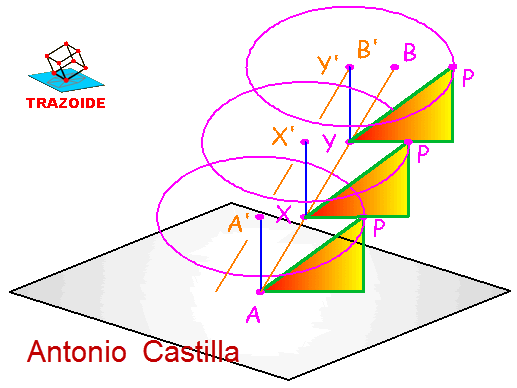
Luego, podemos afirmar que el lugar geométrico de las soluciones que satisfacen el problema es un cilindro oblicuo de eje una recta paralela a AB (la A'-B' del esquema anterior) dos metros (medidos en vertical) por encima de esta y de directriz una circunferencia de radio 100 metros.
Como la solución también debe estar sobre la recta CD (esquema inferior) se hallará donde CD atraviese al cilindro.
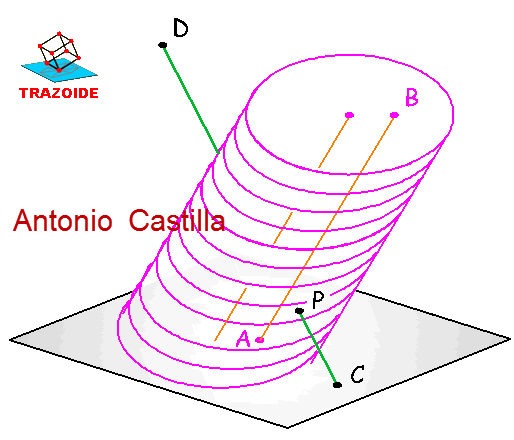
Voy a dar una explicación de mi razonamiento. Los dibujos que ofrezco son esquemas, no es el dibujo real, ni están hechos con medidas.
El razonamiento y los esquemas que doy son en el espacio, no aplicando el sistema acotado.
RAZONAMIENTO :
Supongamos que sobre el plano horizontal tengo el punto A (ver el esquema debajo de este párrafo). A partir de él levanto una recta con una pendiente del 2% y localizo sobre ella el punto P, que está dos metros por encima del punto A. La proyección de esa recta, AP, es el cateto horizontal de 100 m de largo.

Ahora bien, existen infinitas posiciones para la recta AP, que se consiguen al girar el triángulo de la pendiente alrededor de A. Cualquiera de esos puntos sería una solución, luego todos los posibles puntos (lugar geométrico) que son solución forman una circunferencia de radio 100 m y centro 2 m por encima del punto A (la circunferencia magenta en el siguiente esquema).

Pero, claro está, no va a dar la casualidad de que la recta que buscamos parta del punto A (dado en el enunciado), sino que saldrá de otro que esté sobre la recta AB. Es por eso que puedo aplicar idéntico razonamiento a todos los infinitos puntos entre A y B. Esto dará infinitas circunferencias donde estarán las posibles soluciones (perdonar que no haya dibujado las infinitas circunferencias y me haya conformado con solo tres en el esquema siguiente).

Luego, podemos afirmar que el lugar geométrico de las soluciones que satisfacen el problema es un cilindro oblicuo de eje una recta paralela a AB (la A'-B' del esquema anterior) dos metros (medidos en vertical) por encima de esta y de directriz una circunferencia de radio 100 metros.
Como la solución también debe estar sobre la recta CD (esquema inferior) se hallará donde CD atraviese al cilindro.

- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
La solución en el sistema acotado es esta :
Construyo un cilindro de eje una paralela a AB, dos metros por encima y con una directriz circular de radio 100 m. En realidad para el eje no hago nada, pues su proyección es la misma que AB, la única diferencia es que la cota de sus puntos es 2 m más alta.
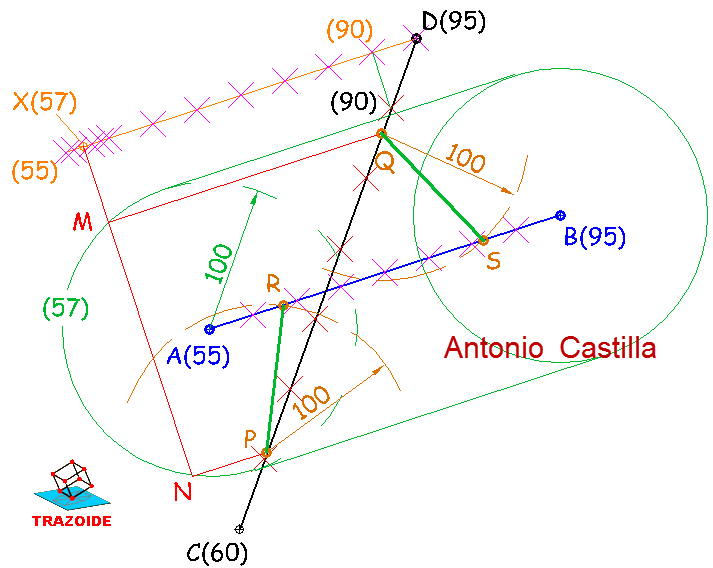
Por cualquiera de los puntos de CD (en mi caso por el que está encima de A, que tiene cota 55 + 2 = 57 m) trazas una directriz de radio 100 m. Yo he dibujado el cilindro completo, pero con la directriz es bastante.
Hallo la intersección de la recta CD con el cilindro. Te recuerdo el método : Por un punto cualquiera de CD (en mi caso por D) trazas una paralela al eje del cilindro. Es decir, haces una paralela a AB.
Gradúas esa paralela con el mismo intervalo que AB.
Planteas el plano formado por CD y la paralela al eje del cilindro. En mi dibujo he unido los puntos de cota 90 y ya tengo una línea de cota del plano.
La solución en el sistema acotado es esta :
Construyo un cilindro de eje una paralela a AB, dos metros por encima y con una directriz circular de radio 100 m. En realidad para el eje no hago nada, pues su proyección es la misma que AB, la única diferencia es que la cota de sus puntos es 2 m más alta.

Por cualquiera de los puntos de CD (en mi caso por el que está encima de A, que tiene cota 55 + 2 = 57 m) trazas una directriz de radio 100 m. Yo he dibujado el cilindro completo, pero con la directriz es bastante.
Hallo la intersección de la recta CD con el cilindro. Te recuerdo el método : Por un punto cualquiera de CD (en mi caso por D) trazas una paralela al eje del cilindro. Es decir, haces una paralela a AB.
Gradúas esa paralela con el mismo intervalo que AB.
Planteas el plano formado por CD y la paralela al eje del cilindro. En mi dibujo he unido los puntos de cota 90 y ya tengo una línea de cota del plano.
-
Jose Maroto
- USUARIO

- Mensajes: 6
- Registrado: Sab, 14 Ene 2012, 16:31
La solución a ese enunciado es esa, pero ese no es el problema que yo planteo.
En el resuelto conoces la diferencia de cotas entre los dos puntos de enlace, sin embargo, en el problema que planteo solo se conoce la pendiente.
Evidentemente el cono se irá deslizando por la recta superior o inferior, no lo tengo muy claro (por la condiciones de la mayor y menor cota en CD) y las generatrices de los infinitos conos serán rectas con la pendiente pedida. Llegará un momento que uno de los conos sea tangente a la otra recta y empezará a producir soluciones, esto es hasta que uno de los conos (de los que se deslizan por la recta) vuelva a ser tangente y deje de cortar. en ese momento ya no habrá más soluciones. Este es el planteamiento intuitivo.
Ni sé en que recta meter los conos, ni como halar los puntos con mayor y menor cota en CD.
En el resuelto conoces la diferencia de cotas entre los dos puntos de enlace, sin embargo, en el problema que planteo solo se conoce la pendiente.
Evidentemente el cono se irá deslizando por la recta superior o inferior, no lo tengo muy claro (por la condiciones de la mayor y menor cota en CD) y las generatrices de los infinitos conos serán rectas con la pendiente pedida. Llegará un momento que uno de los conos sea tangente a la otra recta y empezará a producir soluciones, esto es hasta que uno de los conos (de los que se deslizan por la recta) vuelva a ser tangente y deje de cortar. en ese momento ya no habrá más soluciones. Este es el planteamiento intuitivo.
Ni sé en que recta meter los conos, ni como halar los puntos con mayor y menor cota en CD.
-
Jose Maroto
- USUARIO

- Mensajes: 6
- Registrado: Sab, 14 Ene 2012, 16:31
pués pensando y pensando creo que he dado con la solución, creo.
Si miro desde arriba (acotados) , donde se corten las dos rectas es el punto en AB que va a ser el vertice del cono.
Calculo la cota de ese vertice y situo un cono con la pendiente que me den.
Corto ese cono con la otra recta y esos puntos unidos son los de mayor y menor cota.
Que unidos con el vertice del cono me da la solución.
Creo.
Si miro desde arriba (acotados) , donde se corten las dos rectas es el punto en AB que va a ser el vertice del cono.
Calculo la cota de ese vertice y situo un cono con la pendiente que me den.
Corto ese cono con la otra recta y esos puntos unidos son los de mayor y menor cota.
Que unidos con el vertice del cono me da la solución.
Creo.
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
He encontrado la solución en un libro, así que coloco el texto y las imágenes tal como vienen. El "traducirlo" te lo dejo a ti para mí ya es muy tarde y me voy a la cama que estoy muerto de sueño.
ENUNCIADO
Dos tuberías de ejes r y s han de unirse por medio de otra tubería cuyo eje corte a r y s y
tenga una pendiente dada pt = 10 %, Para decidir el trazado más idóneo, se desea saber:
a) Soluciones posibles y forma de determinadas.
b) Tuberías de longitud máxima y mínima.
SOLUCIÓN
a) Tracemos el plano definido por la recta r, (Fig. a), por ejemplo, y un punto P de s (no dibujado). Las rectas de pendiente pr, trazadas por P y contenidas en el plano [P, r] son las buscadas. Según que la pendiente del plano sea mayor, igual o menor que pT, existirán dos, una o ninguna solución.
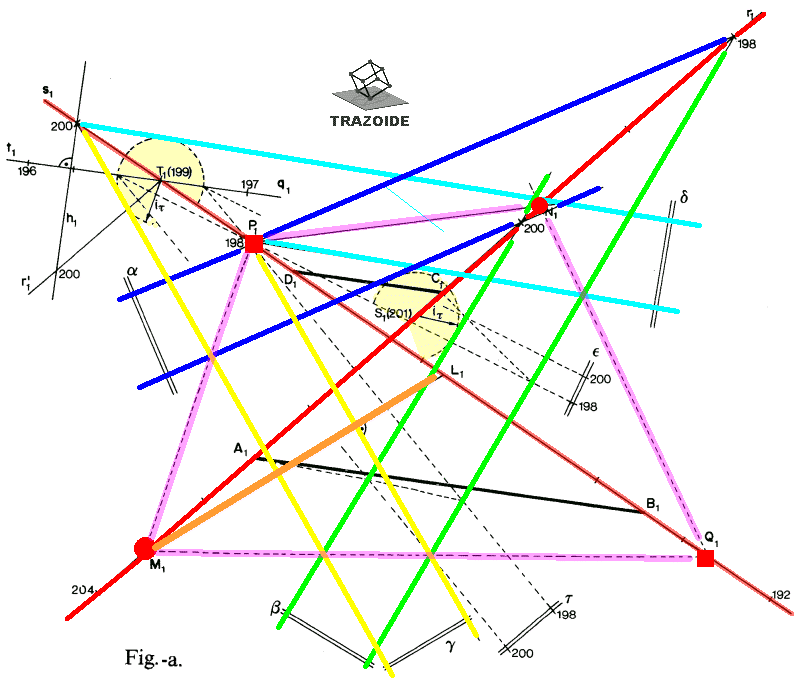
Los planos que limitan las posibles soluciones (planos límites) son los de pendiente pt = 10 % que pasan por r y s, es decir, los planos alfa y beta, que pasan por r y las gamma y delta que pasan por s. Las horizontales de cota 200 de alfa y beta, por ejemplo, son las tangentes a las circunferencias de centro S1 (201) y radio it, trazadas desde el punto de cota 200 de r, siendo it = l/pt = 10 m (a la escala del dibujo). Las intersecciones P y Q de s con alfa y beta y las M y N de r con gamma y delta se obtienen como intersección de recta y plano o por las intersecciones PM, QM y PN, QN de gamma y delta con el diédrico de caras alfa y beta.
El lugar de los extremos de las tuberías buscadas son, por tanto, los segmentos MN y PQ. Así, la tubería límite ML que pasa por M es la recta de máxima pendiente del plano gamma, trazada por M.
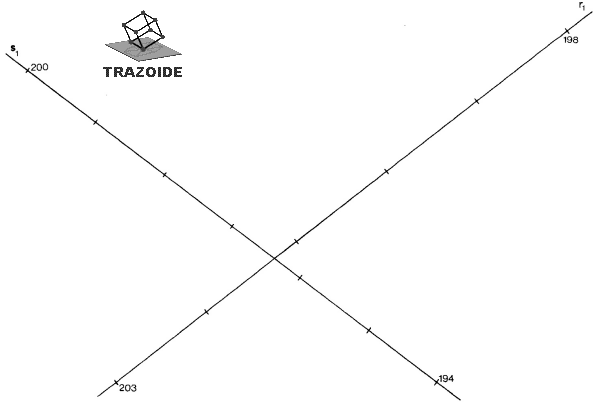
b) Tubería máxima y mínima. Sean r y s las rectas dadas (Fig. b); RS, la perpendicular común; sigma, el plano paralelo a r que contiene a s; H, un plano horizontal arbitrario y AB, el eje de una de las tuberías buscadas. Tracemos por A la vertical n y la perpendicular p a sigma (paralela a RS) que cortan a sigma en E y F, siendo m = EF una recta de máxima pendiente de sigma.
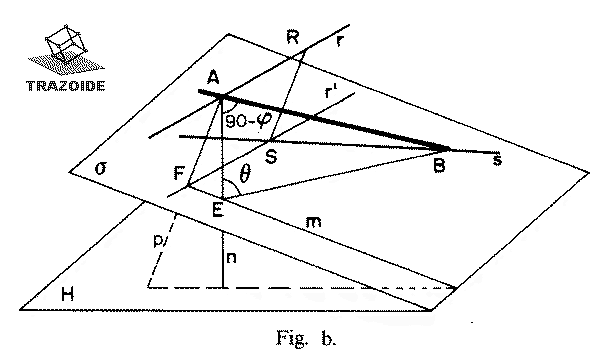
Si unimos E y B, el triángulo AEB tiene el ángulo  constante, de valor  = 90 — phi (siendo phi el ángulo de inclinación de la pendiente pt = 10 %) y el lado AE de longitud constante, por serlo AF = RS, luego AB será de longitud máxima o mínima, según que el ángulo opuesto theta.
sea máximo o mínimo y esto sucede si EB coincide con la proyección ortogonal m de n sobre sigma, es decir, cuando las proyecciones ortogonales de AB y RS sean paralelas. De aquí, la construcción (Fig. a):
Trazar por un punto T1(199) de s, la paralela r’ a r que determina la horizontal h1(200) del plano sigma = [s, r']. La perpendicular común de r y s es normal a sigma y se proyecta
según la normal t1 a h1, luego las tuberías buscadas son las rectas de pendiente pt y proyección paralela a t1 que cortan a r y s. Para hallarlas, se han trazado por el punto
T1(199) de s las rectas q1 y t1 de intervalo it que forman con s los planos epsilón y tau que cortan a r en C y A. Las paralelas a t1, trazadas por estos puntos, son los ejes buscados CD y AB que cortan a s en D y B, respectivamente.
He encontrado la solución en un libro, así que coloco el texto y las imágenes tal como vienen. El "traducirlo" te lo dejo a ti para mí ya es muy tarde y me voy a la cama que estoy muerto de sueño.
ENUNCIADO
Dos tuberías de ejes r y s han de unirse por medio de otra tubería cuyo eje corte a r y s y
tenga una pendiente dada pt = 10 %, Para decidir el trazado más idóneo, se desea saber:
a) Soluciones posibles y forma de determinadas.
b) Tuberías de longitud máxima y mínima.

SOLUCIÓN
a) Tracemos el plano definido por la recta r, (Fig. a), por ejemplo, y un punto P de s (no dibujado). Las rectas de pendiente pr, trazadas por P y contenidas en el plano [P, r] son las buscadas. Según que la pendiente del plano sea mayor, igual o menor que pT, existirán dos, una o ninguna solución.

Los planos que limitan las posibles soluciones (planos límites) son los de pendiente pt = 10 % que pasan por r y s, es decir, los planos alfa y beta, que pasan por r y las gamma y delta que pasan por s. Las horizontales de cota 200 de alfa y beta, por ejemplo, son las tangentes a las circunferencias de centro S1 (201) y radio it, trazadas desde el punto de cota 200 de r, siendo it = l/pt = 10 m (a la escala del dibujo). Las intersecciones P y Q de s con alfa y beta y las M y N de r con gamma y delta se obtienen como intersección de recta y plano o por las intersecciones PM, QM y PN, QN de gamma y delta con el diédrico de caras alfa y beta.
El lugar de los extremos de las tuberías buscadas son, por tanto, los segmentos MN y PQ. Así, la tubería límite ML que pasa por M es la recta de máxima pendiente del plano gamma, trazada por M.
b) Tubería máxima y mínima. Sean r y s las rectas dadas (Fig. b); RS, la perpendicular común; sigma, el plano paralelo a r que contiene a s; H, un plano horizontal arbitrario y AB, el eje de una de las tuberías buscadas. Tracemos por A la vertical n y la perpendicular p a sigma (paralela a RS) que cortan a sigma en E y F, siendo m = EF una recta de máxima pendiente de sigma.

Si unimos E y B, el triángulo AEB tiene el ángulo  constante, de valor  = 90 — phi (siendo phi el ángulo de inclinación de la pendiente pt = 10 %) y el lado AE de longitud constante, por serlo AF = RS, luego AB será de longitud máxima o mínima, según que el ángulo opuesto theta.
sea máximo o mínimo y esto sucede si EB coincide con la proyección ortogonal m de n sobre sigma, es decir, cuando las proyecciones ortogonales de AB y RS sean paralelas. De aquí, la construcción (Fig. a):
Trazar por un punto T1(199) de s, la paralela r’ a r que determina la horizontal h1(200) del plano sigma = [s, r']. La perpendicular común de r y s es normal a sigma y se proyecta
según la normal t1 a h1, luego las tuberías buscadas son las rectas de pendiente pt y proyección paralela a t1 que cortan a r y s. Para hallarlas, se han trazado por el punto
T1(199) de s las rectas q1 y t1 de intervalo it que forman con s los planos epsilón y tau que cortan a r en C y A. Las paralelas a t1, trazadas por estos puntos, son los ejes buscados CD y AB que cortan a s en D y B, respectivamente.
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 15 invitados

