Hallar el lugar geométrico de los puntos P cuando varía r *
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
Hallar el lugar geométrico de los puntos P cuando varía r *
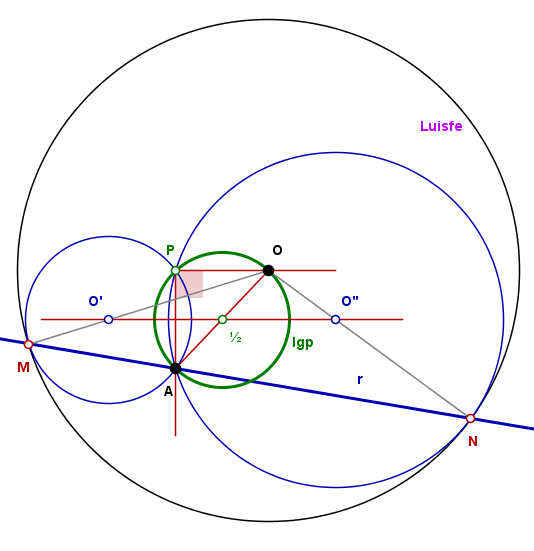
Por A se trazan una serie de rectas r que cortan a (O) en los puntos M y N. Trazar la circunferencia (O') que pasa por A y es tangente a (O) en M y otra circunferencia (O'') que pase por A y sea tangente a (O) en N. El punto de intersección de las circunferencias (O') y (O'') es P. Hallar el lugar geométrico de los puntos P cuando varía r.
DATOS: Circunferencia (O) y el punto A, que es interior a ella y está sobre r (infinitas rectas r).
DATOS: Circunferencia (O) y el punto A, que es interior a ella y está sobre r (infinitas rectas r).
¡Gracias! por lo de genio, pero yo el único genio que tengo es... :twisted: cuando me enfado mucho 
Bueno, los lugares geométricos es más fácil presuponer y a además acertar que demostrarlos con una base matemática sólida y ordenada. Para ésto último hace falta cierta dedicación, tiempo y ganas.
Para mí los Puntos A y O son perfectamente demostrables si colocas la cuerda alineada con A y O y también transversalmente.
Luego para no pensar que pueda ser una elipse observo que para cualquier posición el ángulo APO es siempre recto , siendo
siempre PO paralela a la unión de O'O" y PA transversal como buen eje radical que es (a O'O").
Se pueden buscar otras explicaciones como que P es simétrico de A respecto a la recta O'O" y que ésta gira en el punto medio de O'O" (tb. OA).
Éste lugar geométrico ya lo conocemos.
Ya sé que no es una explicación muy satisfactoria, pero repito, hace falta tiempo para ello.
NOTA: Tú que lo estás estudiando ahora, no estaría mal que si tienes acceso a una explicación mejor, no te olvides de pasarte por
aquí y añadir tus comentarios
Saludos.
.
Bueno, los lugares geométricos es más fácil presuponer y a además acertar que demostrarlos con una base matemática sólida y ordenada. Para ésto último hace falta cierta dedicación, tiempo y ganas.
Para mí los Puntos A y O son perfectamente demostrables si colocas la cuerda alineada con A y O y también transversalmente.
Luego para no pensar que pueda ser una elipse observo que para cualquier posición el ángulo APO es siempre recto , siendo
siempre PO paralela a la unión de O'O" y PA transversal como buen eje radical que es (a O'O").
Se pueden buscar otras explicaciones como que P es simétrico de A respecto a la recta O'O" y que ésta gira en el punto medio de O'O" (tb. OA).
Éste lugar geométrico ya lo conocemos.
Ya sé que no es una explicación muy satisfactoria, pero repito, hace falta tiempo para ello.
NOTA: Tú que lo estás estudiando ahora, no estaría mal que si tienes acceso a una explicación mejor, no te olvides de pasarte por
aquí y añadir tus comentarios
Saludos.
.
Todo lo que encontremos constante en las diferentes posiciones de la cuerda, es un buen comienzo,
pero creo que lo que dices es un poco lo que ya te estoy contando. Si te has fijado bien en el dibujo marco el ángulo de 90º
que se que es constante por las razones que te he explicado más arriba.
También se puede comenzar al revés, dibujando el supuesto lugar geométrico y seguir trazando en sentido contrario para
encontrar sentido a nuestra hipótesis.
Nota: olvidé dibujar la línea O'O" en el dibujo (lo editaré), seguro que con ella se entiende más por donde van los tiros.
Yo por mi parte, dejo en tus manos y en las del foro cualquier mejora al tema.
Ahora voy a editar el dibujo de la elipse en el otro post, que olvidé nombrar algún punto y también hacer unas observaciones.
Saludos.
pero creo que lo que dices es un poco lo que ya te estoy contando. Si te has fijado bien en el dibujo marco el ángulo de 90º
que se que es constante por las razones que te he explicado más arriba.
También se puede comenzar al revés, dibujando el supuesto lugar geométrico y seguir trazando en sentido contrario para
encontrar sentido a nuestra hipótesis.
Nota: olvidé dibujar la línea O'O" en el dibujo (lo editaré), seguro que con ella se entiende más por donde van los tiros.
Yo por mi parte, dejo en tus manos y en las del foro cualquier mejora al tema.
Ahora voy a editar el dibujo de la elipse en el otro post, que olvidé nombrar algún punto y también hacer unas observaciones.
Saludos.
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 12 invitados