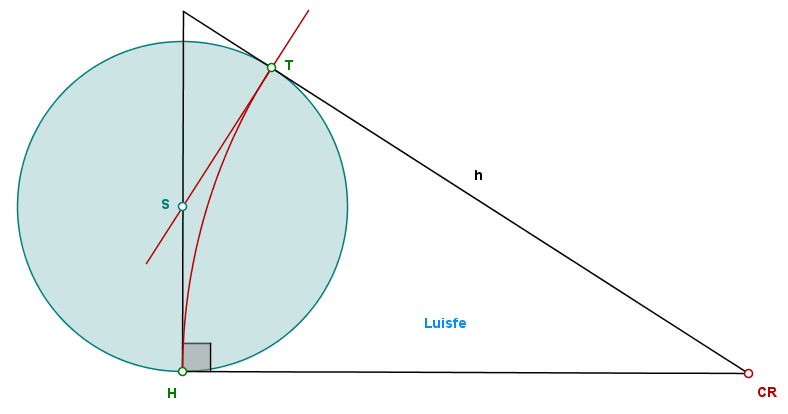
Dado un triángulo rectángulo, construir una circunferencia tangente a la hipotenusa, que pase por el vértice del ángulo recto y que tenga su centro en uno de los catetos
Me han dicho que es muy simple y que no hace falta ni inversion ni nada de eso pero no doy con ello, ¡una ayudita! plis
circunferencia tangente a la hipotenusa, que pase por el vértice del ángulo recto*
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí) El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
Por supuesto, la solución de Luisfe es más rápida y simple, pero yo voy a proponer otra mediante una homotecia.
1 - Dibujar una circunferencia cualquiera con centro cualquiera sobre un cateto, O' y radio hasta el ángulo recto, H.
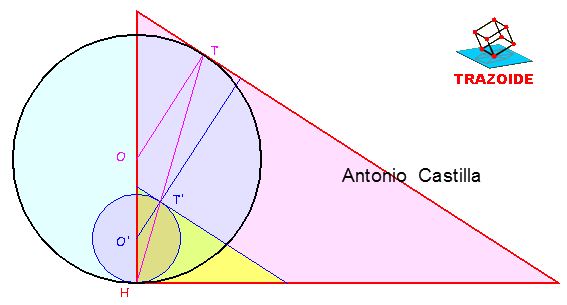
2 - Desde su centro, O', dibujar una perpendicular a la hipotenusa, que nos da el punto de tangencia, T', en un triángulo homotético al dado (el triángulo relleno de amarillo, aunque no hace falta dibujarlo).
3 - Unir el ángulo recto H (el centro de homotecia) con el punto de tangencia T' y donde corte a la hipotenusa es el punto de tangencia de la circunferencia buscada, T.
4 - Por el punto de tangencia, T, trazar una perpendicular a la hipotenusa y obtenemos el centro de la circunferencia buscada, O.
Por supuesto, la solución de Luisfe es más rápida y simple, pero yo voy a proponer otra mediante una homotecia.
1 - Dibujar una circunferencia cualquiera con centro cualquiera sobre un cateto, O' y radio hasta el ángulo recto, H.

2 - Desde su centro, O', dibujar una perpendicular a la hipotenusa, que nos da el punto de tangencia, T', en un triángulo homotético al dado (el triángulo relleno de amarillo, aunque no hace falta dibujarlo).
3 - Unir el ángulo recto H (el centro de homotecia) con el punto de tangencia T' y donde corte a la hipotenusa es el punto de tangencia de la circunferencia buscada, T.
4 - Por el punto de tangencia, T, trazar una perpendicular a la hipotenusa y obtenemos el centro de la circunferencia buscada, O.
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 18 invitados