representar un cubo
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
-
estudiante_us
- USUARIO

- Mensajes: 3
- Registrado: Sab, 11 Oct 2008, 14:22
representar un cubo
El enunciado dice así:
Representar las proyecciones diédricas del cubo de diagonal AB (no es diagonal de cara sino del cubo) y de su esfera inscrita, señalando el punto de tangencia entre ambos. Y sabiendo tambien que hay un vértice contenido en el plano de proyección horizontal y sera el de mayor alejamiento. El punto A tiene de coordenadas (11.5, 0, 5) y B(6.5, 9, 5)
He comenzado con cambios de plano pero no sé como seguir puesto que no encuentro la posición del vértice contenido en el PH o la sección principal.
Mucha gracias
Representar las proyecciones diédricas del cubo de diagonal AB (no es diagonal de cara sino del cubo) y de su esfera inscrita, señalando el punto de tangencia entre ambos. Y sabiendo tambien que hay un vértice contenido en el plano de proyección horizontal y sera el de mayor alejamiento. El punto A tiene de coordenadas (11.5, 0, 5) y B(6.5, 9, 5)
He comenzado con cambios de plano pero no sé como seguir puesto que no encuentro la posición del vértice contenido en el PH o la sección principal.
Mucha gracias
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
El problema con las medidas que das no tiene solución, o al menos no puede tener un vértice apoyado en el plano horizontal de proyección. Para solucionarlo yo le he quitado 10 mm a las medidas de las cotas de los puntos A y B. La forma de resolverlo es la que te comento a continuación, independientemente de cuanto sea la medida.
SOLUCIÓN
1 - Comenzaremos por situar los puntos A y B por sus coordenadas.
2 - AB forma una recta horizontal, por lo que su proyección horizontal es la verdadera magnitud de la longitud de la diagonal principal.
3 - Conocida la verdadera magnitud de la diagonal principal, necesitamos las restantes medidas para conocer la sección principal. En el siguiente mensaje te recuerdo como se haya.
El problema con las medidas que das no tiene solución, o al menos no puede tener un vértice apoyado en el plano horizontal de proyección. Para solucionarlo yo le he quitado 10 mm a las medidas de las cotas de los puntos A y B. La forma de resolverlo es la que te comento a continuación, independientemente de cuanto sea la medida.
SOLUCIÓN
1 - Comenzaremos por situar los puntos A y B por sus coordenadas.
2 - AB forma una recta horizontal, por lo que su proyección horizontal es la verdadera magnitud de la longitud de la diagonal principal.
3 - Conocida la verdadera magnitud de la diagonal principal, necesitamos las restantes medidas para conocer la sección principal. En el siguiente mensaje te recuerdo como se haya.
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
Determinación de las magnitudes de un cubo (lado y diagonal de cara) conocida la diagonal principal o de cuerpo
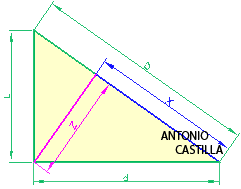
4 - Se dibuja un triángulo rectángulo de catetos idénticos e iguales a una cantidad elegida al azar, L'. La hipotenusa del triángulo es el valor de la diagonal de cara, d', del cubo que tuviese por lado la longitud L'
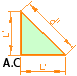
5 - Se construye un nuevo triángulo rectángulo de catetos iguales a la longitud L' y d'. Este triángulo es equivalente a haber dibujado la sección principal del cubo, por lo que la hipotenusa es equivalente a la diagonal principal, D'
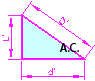
6 - Se coloca sobre la hipotenusa del último triángulo el valor de la diagonal principal, D, y mediante paralelas a los lados del triángulo se trazan dos nuevos catetos. El cateto menor es la longitud de la arista del cubo, L, mientras que el mayor es la longitud de la diagonal de cara, d. Recuérdese que este triángulo es media sección principal.
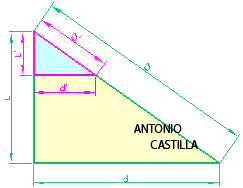
Determinación de las magnitudes de un cubo (lado y diagonal de cara) conocida la diagonal principal o de cuerpo
4 - Se dibuja un triángulo rectángulo de catetos idénticos e iguales a una cantidad elegida al azar, L'. La hipotenusa del triángulo es el valor de la diagonal de cara, d', del cubo que tuviese por lado la longitud L'

5 - Se construye un nuevo triángulo rectángulo de catetos iguales a la longitud L' y d'. Este triángulo es equivalente a haber dibujado la sección principal del cubo, por lo que la hipotenusa es equivalente a la diagonal principal, D'

6 - Se coloca sobre la hipotenusa del último triángulo el valor de la diagonal principal, D, y mediante paralelas a los lados del triángulo se trazan dos nuevos catetos. El cateto menor es la longitud de la arista del cubo, L, mientras que el mayor es la longitud de la diagonal de cara, d. Recuérdese que este triángulo es media sección principal.

- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
Representar un cubo, conocida su diagonal principal, AB, que es una recta horizontal, estando el vértice c sobre el plano horizontal de proyección
7 - Se realiza un cambio de plano del segmento AB, con la segunda línea de tierra, L.T-2, perpendicular a la proyección horizontal de AB
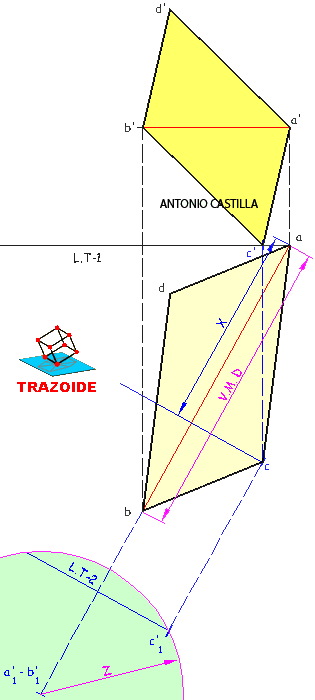
8 - Sobre la media sección principal obtenida antes, se dibuja una perpendicular a la hipotenusa que pase por el vértice del ángulo recto. Esto nos da la medida Z
9 - En el cambio de plano, con radio Z y centro en A'1-B'1, se traza un arco. Donde este arco corte a la línea de tierra es el vértice C'1

10 - De nuevo en la media sección principal se mide la longitud X, que hay entre un extremo y el punto por el que se hizo la perpendicular a la hipotenusa.

11 - Desde el extremo A de la proyección horizontal de A-B se mide la distancia X, y por ese punto se dibuja una perpendicular a A-B
12 - Mediante una perpendicular a la segunda línea de tierra, L.T-2, que parta de C'1 se consigue la proyección horizontal de C en la perpendicular del apartado anterior.

13 - La proyección vertical de C estará sobre la línea de tierra primera, L.T 1
14 - Por la proyección horizontal de A se hace una paralela a B-C, y por el extremo B otra paralela a A-C. Donde se corten es otro vértice del cubo, D
15 - A-C-B-D es la sección principal del cubo. Repetir en la proyección vertical.
A partir de aquí solo resta levantar el cuerpo. Imagino que eso ya lo sabes.
Representar un cubo, conocida su diagonal principal, AB, que es una recta horizontal, estando el vértice c sobre el plano horizontal de proyección
7 - Se realiza un cambio de plano del segmento AB, con la segunda línea de tierra, L.T-2, perpendicular a la proyección horizontal de AB

8 - Sobre la media sección principal obtenida antes, se dibuja una perpendicular a la hipotenusa que pase por el vértice del ángulo recto. Esto nos da la medida Z

9 - En el cambio de plano, con radio Z y centro en A'1-B'1, se traza un arco. Donde este arco corte a la línea de tierra es el vértice C'1

10 - De nuevo en la media sección principal se mide la longitud X, que hay entre un extremo y el punto por el que se hizo la perpendicular a la hipotenusa.

11 - Desde el extremo A de la proyección horizontal de A-B se mide la distancia X, y por ese punto se dibuja una perpendicular a A-B
12 - Mediante una perpendicular a la segunda línea de tierra, L.T-2, que parta de C'1 se consigue la proyección horizontal de C en la perpendicular del apartado anterior.

13 - La proyección vertical de C estará sobre la línea de tierra primera, L.T 1
14 - Por la proyección horizontal de A se hace una paralela a B-C, y por el extremo B otra paralela a A-C. Donde se corten es otro vértice del cubo, D
15 - A-C-B-D es la sección principal del cubo. Repetir en la proyección vertical.
A partir de aquí solo resta levantar el cuerpo. Imagino que eso ya lo sabes.
-
estudiante_us
- USUARIO

- Mensajes: 3
- Registrado: Sab, 11 Oct 2008, 14:22
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 23 invitados

