Mensaje sin leer
por Antonio Briones » Mar, 31 Dic 2013, 11:21
Hola, Luisfe.
Ciertamente, bastaba con eso para que el problema se remitiera a "Parábola conocidas tres tangentes y dos de sus puntos de tangencia".
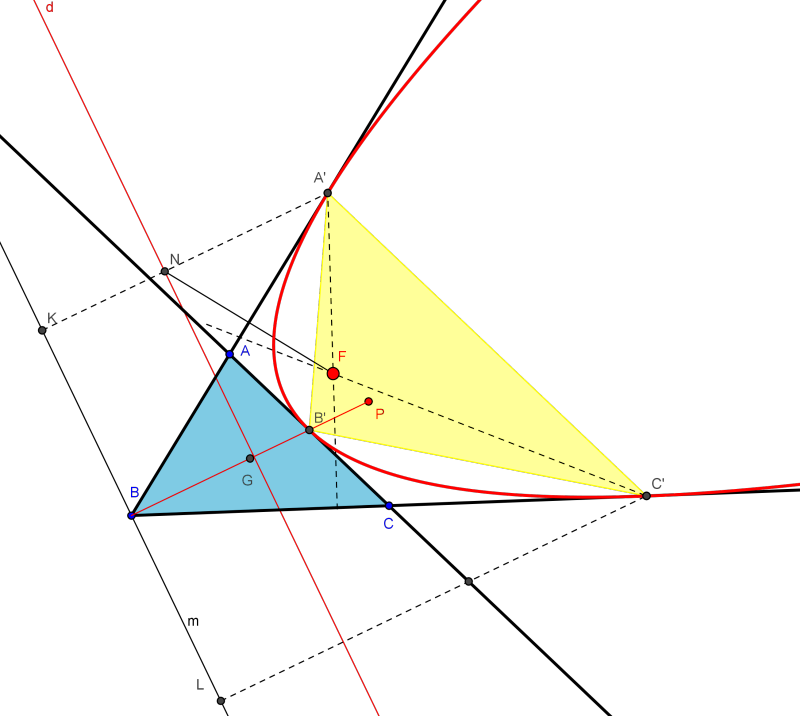
Otro aspecto importante es, además, que a 3 tangentes cualesquiera, sin especificar los puntos de tangencia, pueden inscribírseles muchas parábolas. Creo que para que la parábola sea única es necesario dar, el menos un punto de contacto, problema que tampoco aparece en Trazoide, y cuya solución intentaré aportar cuando vuelva de vacaciones.
Lo que yo expongo en mi post es un caso particular de esto último: la parábola tangente a 3 rectas dado como punto de tangencia P el medio del segmento que queda entre dos de ellas. Tiene, además, de particular que su perspector es la intersección de la elipse de Steiner exterior a ABC con la prolongación de la mediana que pasa por P.
Feliz Año.


 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado




