triángulo ABC conociendo la diferencia de las proyecciones de los lados *
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
triángulo ABC conociendo la diferencia de las proyecciones de los lados *
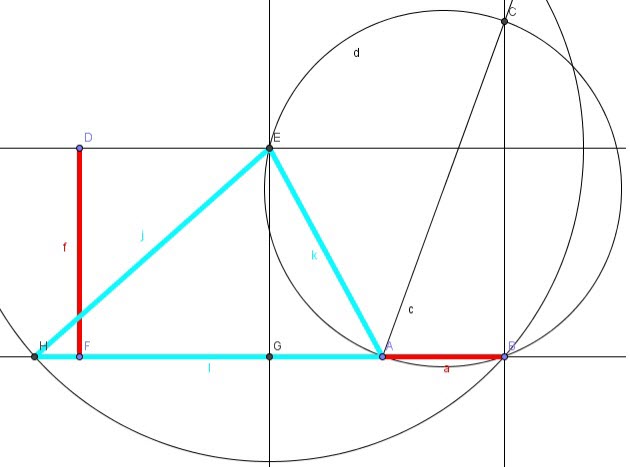
Construir un triángulo ABC conociendo la diferencia b'-c' de las proyecciones de los lados b y c sobre a, la diferencia B-C y la altura correspondiente al lado BC, ha.
un ejercicio que me tienen hecho un lio gracias a todos
un ejercicio que me tienen hecho un lio gracias a todos
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
Parece que el problema ha captado la atención de mucha gente y Seroig se ha adelantado.
Mi solución creo que es prácticamente la misma, pero ya que he "perdido" el tiempo en hacer los dibujos para dar una explicación la colocó y así complemento un poco más el ejercicio.
Primero la solución :
1 - Se traza el segmento AA' diferencia de las proyecciones.
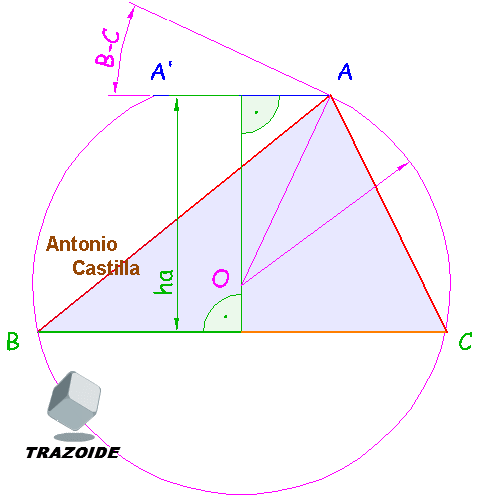
2 - Respecto de AA' se dibuja el arco capaz de la diferencia de los ángulos, B-C.
3 - Con una paralela a AA' a una distancia la de la altura dada, ha, se traza otra recta.
4 - Donde esta última corte al arco capaz son los vértices B y C. Unirlos con uno de los extremos de AA'.
El fundamento :
a - Imaginemos el triángulo ya construido ABC y su simétrico, A'BC, respecto de la mediatriz de BC.
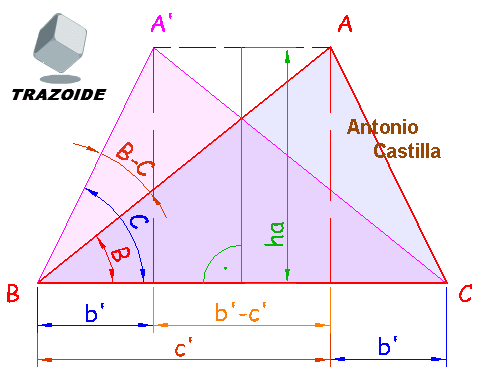
b - Proyectemos los lados b y c (de ABC) sobre el lado a obteniendo b' y c'.
c - Proyectemos ahora también los mismos lados pero del triángulo simétrico, A'BC.
d - Podemos comprobar fácilmente que la distancia entre los dos simétricos AA' es la diferencia entre las proyecciones b'-c'.
e - Por otro lado si nos fijamos en el lado izquierdo para el triángulo ABC tenemos el ángulo B, y para el triángulo A'BC el ángulo que hay es C. Y en el triángulo BA'A el ángulo es la diferencia C-B.
f - Resumiendo del triángulo BA'A conocemos uno de sus lados AA' = b'-c', uno de sus ángulos A'BA = C-B y una de sus alturas ha, luego el problema se soluciona resolviendo ese triángulo.
Parece que el problema ha captado la atención de mucha gente y Seroig se ha adelantado.
Mi solución creo que es prácticamente la misma, pero ya que he "perdido" el tiempo en hacer los dibujos para dar una explicación la colocó y así complemento un poco más el ejercicio.
Primero la solución :
1 - Se traza el segmento AA' diferencia de las proyecciones.

2 - Respecto de AA' se dibuja el arco capaz de la diferencia de los ángulos, B-C.
3 - Con una paralela a AA' a una distancia la de la altura dada, ha, se traza otra recta.
4 - Donde esta última corte al arco capaz son los vértices B y C. Unirlos con uno de los extremos de AA'.
El fundamento :
a - Imaginemos el triángulo ya construido ABC y su simétrico, A'BC, respecto de la mediatriz de BC.

b - Proyectemos los lados b y c (de ABC) sobre el lado a obteniendo b' y c'.
c - Proyectemos ahora también los mismos lados pero del triángulo simétrico, A'BC.
d - Podemos comprobar fácilmente que la distancia entre los dos simétricos AA' es la diferencia entre las proyecciones b'-c'.
e - Por otro lado si nos fijamos en el lado izquierdo para el triángulo ABC tenemos el ángulo B, y para el triángulo A'BC el ángulo que hay es C. Y en el triángulo BA'A el ángulo es la diferencia C-B.
f - Resumiendo del triángulo BA'A conocemos uno de sus lados AA' = b'-c', uno de sus ángulos A'BA = C-B y una de sus alturas ha, luego el problema se soluciona resolviendo ese triángulo.
Hola.
Había interpretado mal el ejercicio. Por diferencia de B-C entendí diferencia de lados b-c. Ahora viendo las
respuestas de Antonio y Seroig caigo en la cuenta de que se trataba de la diferencia de ángulos B-C. En fin, no se puede estar a mil cosas a la vez. Por lo tanto, mi solución no la subo ya que no corresponde a éste enunciado. !Que pena!, había hecho un triángulo muy mono
Saludos compañeros.
Había interpretado mal el ejercicio. Por diferencia de B-C entendí diferencia de lados b-c. Ahora viendo las
respuestas de Antonio y Seroig caigo en la cuenta de que se trataba de la diferencia de ángulos B-C. En fin, no se puede estar a mil cosas a la vez. Por lo tanto, mi solución no la subo ya que no corresponde a éste enunciado. !Que pena!, había hecho un triángulo muy mono
Saludos compañeros.
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 6 invitados