.
Hace tiempo que no resolvía problemas de este tipo y mis conocimientos se oxidan, así que para quitarle el polvo a mis neuronas probé a realizarlo de otra forma. No sé si esto escapará de tus conocimientos pero servirá para otras personas.
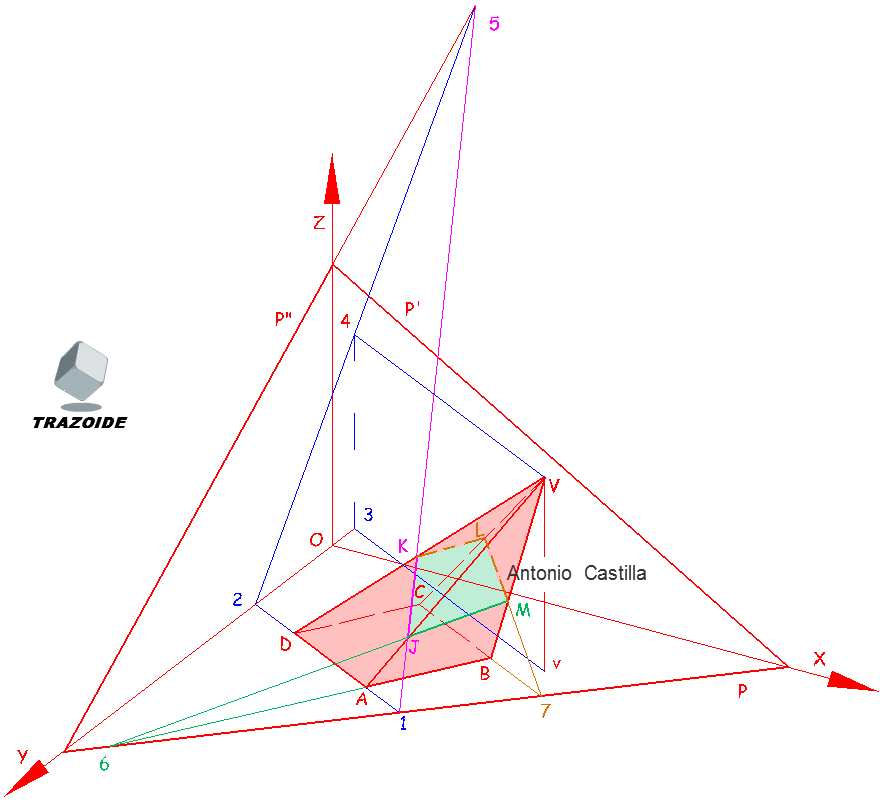
a - Lo resolveré planteando una homología proyectada sobre el plano XY. La proyección secundaria de V es el centro de homología, la traza p del plano es el eje de homología y la base ABCD es la figura a transformar.
b - Nos falta un elemento más, en este caso la recta límite. Para hallarla se dibuja un plano paralelo al dado pasando por el vértice de la pirámide. Como las trazas serán paralelas solo hace falta una recta y su traza. Por V dibujo una paralela a p' y por v una paralela al eje X (he dibujado una recta del plano y su proyección). Su traza, punto 10, es un punto de la traza del plano, p2, paralela a p y recta límite de la homología.
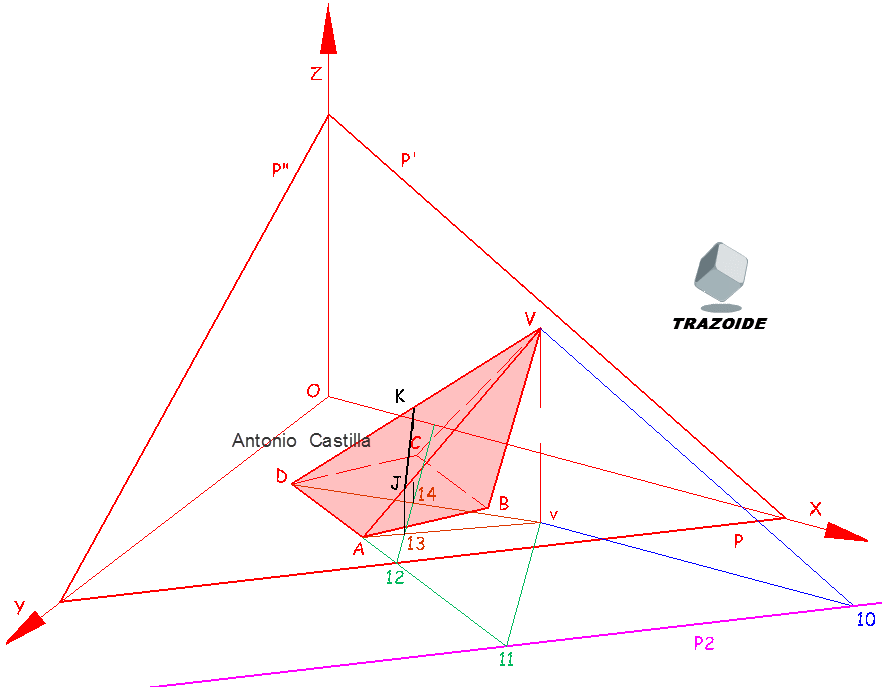
c - Se resuelve la homología. Prolongar AD hasta la recta límite p2 (punto 11) y uniéndolo con el centro de homología v se obtiene la dirección, 11-v, de la homóloga de AD.
d - Donde AD corta al eje de homología p (punto 12) se traza una paralela a 11-v y esta es la homóloga de AD.
e - Donde esta última corte a las uniones de A y D con V son los puntos, 13 y 14, de la intersección proyectados sobre el plano XY. Subirlos a las proyecciones principales con paralelas al eje Z y nos dan los puntos J y K de la sección.
f - Se puede repetir con los demás o seguir la homología espacial que planteé a partir del apartado 5 de la resolución anterior.
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí) El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado