CIRCUNFERENCIA QUE PASA POR PAR DE PUNTOS INVERSOS. *
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
-
YoliPocket
- USUARIO

- Mensajes: 0
- Registrado: Jue, 06 Feb 2014, 00:07
CIRCUNFERENCIA QUE PASA POR PAR DE PUNTOS INVERSOS. *
DEMOSTRAR QUE UNA CIRCUNFERENCIA QUE PASA POR 2 PARES DE PUNTOS INVERSOS ES ORTOGONAL (CORTA CON ÁNGULO DE 90º) A LA CIRCUNFERENCIA DE INVERSIÓN.
Hola.
Si irme a las matemáticas puras y duras y echando mano de propiedades gráficas más básicas de la inversión te diré:
La recta que une un par de inversos pasa por su centro de inversión O
Con otro par de inversos tendremos otra recta que igualmente pasa éste centro O .
Las dos rectas por tanto se cruzan en el centro de inversión O.
En una circunferencia con 2 pares de inversos en ella se puede asegurar que es autoinversa, ya que cualquier recta desde el centro O cortará (por propiedad) en un par de inversos
Bien sabido es que el segmento desde le centro O tangente a ésta circunferencia, el segmento OTT' (doble) define la raíz de la potencia de inversión.
y por tanto es radio de la circ. inversión. (cpd = circunferencia de puntos dobles)
Por tanto ambas circunferencias se cortarán ortogonalmente.
Espero que tu le eches las matemáticas que falten.
Saludos.
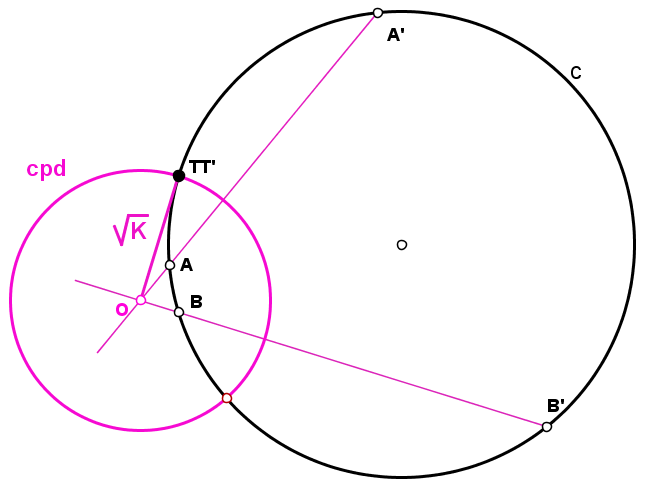
Si irme a las matemáticas puras y duras y echando mano de propiedades gráficas más básicas de la inversión te diré:
La recta que une un par de inversos pasa por su centro de inversión O
Con otro par de inversos tendremos otra recta que igualmente pasa éste centro O .
Las dos rectas por tanto se cruzan en el centro de inversión O.
En una circunferencia con 2 pares de inversos en ella se puede asegurar que es autoinversa, ya que cualquier recta desde el centro O cortará (por propiedad) en un par de inversos
Bien sabido es que el segmento desde le centro O tangente a ésta circunferencia, el segmento OTT' (doble) define la raíz de la potencia de inversión.
y por tanto es radio de la circ. inversión. (cpd = circunferencia de puntos dobles)
Por tanto ambas circunferencias se cortarán ortogonalmente.
Espero que tu le eches las matemáticas que falten.
Saludos.

-
YoliPocket
- USUARIO

- Mensajes: 0
- Registrado: Jue, 06 Feb 2014, 00:07
Así es, todo lo que dijiste es muy cierto O: pero no entiendo porqué el segmento OTT', que es el radio de la circunferencia cpd y que define la razón de potencia de inversión, implique que será ortogonal con el radio de la otra circunferencia por TT'. Es decir, por qué el ángulo <OTT'D=90º??? (Suponiendo que D es el centro de la circunferencia que pasa por A,B,A' y B'.
-
YoliPocket
- USUARIO

- Mensajes: 0
- Registrado: Jue, 06 Feb 2014, 00:07
Piénsalo al revés. Lo que te cuento es materia archidemostrada en cualquier libro de geometría, y no es mi intención
volver a aquello de los triángulos semejantes para explicar el fundamente de potencia o inversión (2 caras de la misma moneda)
Elige un punto del plano cualquiera y "corónale" como centro de inversión O y considera una circunferencia cualquiera que casualmente pasaba por allí.
Cualquier recta "atrevida" que pase por O secante a la circunferencia la cortará "despiadadamente" en un par de puntos, por ejemplo, A, A'.de manera que se cumple que OA*OA'=K. Otra recta "que se uniera a la fiesta", la cortará en B y B' y también se cumple que OB*OB' = K. Parece que K va a ser un "tipo importante". K "acérrimo a sus ideas" es constante para cualquier par de puntos de corte en la circunferencia. Si la recta es tangente, vamos a decir aunque éste mal dicho, que la corta en 2 puntos T,T' "infinitamente juntos" o "juntos para siempre" como dice la canción, entonces se cumple igualmente que OT*OT' = K y como T=T' entonces OT^2 = K y finalmente OT= raíz2(K).
Es decir, la recta que "corta" a la circunferencia en un punto doble de ella, no puede ser otra cosa que una recta tangente a ella con lo que OT (OT'), define la inversión como hemos dicho y se puede considerar por tanto "nada más y nada menos" que el radio de la "auténtica y genuina" circunferencia de inversión o cpd (circ puntos dobles).
"Al final de la historia y sin lamentar más incidentes", llegamos a la conclusión, de que las dos circunferencias, tanto la cpd como la que pasaba por allí, se CORTAN ORTOGONALMENTE.
NOTA: la circunferencia "casual" es doble pero la "pobre" sólo tiene 2 puntos dobles, los de tangencia respecto al centro de inversión (es una circunferencia doble, autoinversa o inversa sí misma y un pelín "egoísta").
"Colorín colorado éste cuento se ha acabado"
Saludos.
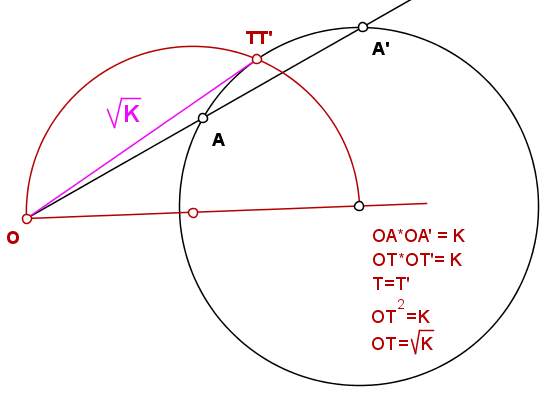
volver a aquello de los triángulos semejantes para explicar el fundamente de potencia o inversión (2 caras de la misma moneda)
Elige un punto del plano cualquiera y "corónale" como centro de inversión O y considera una circunferencia cualquiera que casualmente pasaba por allí.
Cualquier recta "atrevida" que pase por O secante a la circunferencia la cortará "despiadadamente" en un par de puntos, por ejemplo, A, A'.de manera que se cumple que OA*OA'=K. Otra recta "que se uniera a la fiesta", la cortará en B y B' y también se cumple que OB*OB' = K. Parece que K va a ser un "tipo importante". K "acérrimo a sus ideas" es constante para cualquier par de puntos de corte en la circunferencia. Si la recta es tangente, vamos a decir aunque éste mal dicho, que la corta en 2 puntos T,T' "infinitamente juntos" o "juntos para siempre" como dice la canción, entonces se cumple igualmente que OT*OT' = K y como T=T' entonces OT^2 = K y finalmente OT= raíz2(K).
Es decir, la recta que "corta" a la circunferencia en un punto doble de ella, no puede ser otra cosa que una recta tangente a ella con lo que OT (OT'), define la inversión como hemos dicho y se puede considerar por tanto "nada más y nada menos" que el radio de la "auténtica y genuina" circunferencia de inversión o cpd (circ puntos dobles).
"Al final de la historia y sin lamentar más incidentes", llegamos a la conclusión, de que las dos circunferencias, tanto la cpd como la que pasaba por allí, se CORTAN ORTOGONALMENTE.
NOTA: la circunferencia "casual" es doble pero la "pobre" sólo tiene 2 puntos dobles, los de tangencia respecto al centro de inversión (es una circunferencia doble, autoinversa o inversa sí misma y un pelín "egoísta").
"Colorín colorado éste cuento se ha acabado"
Saludos.

-
YoliPocket
- USUARIO

- Mensajes: 0
- Registrado: Jue, 06 Feb 2014, 00:07
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 12 invitados


