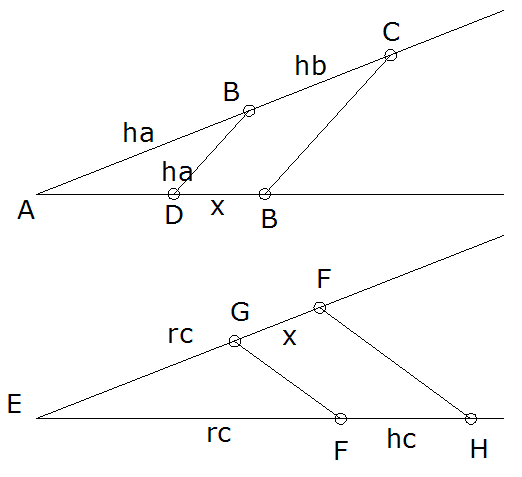
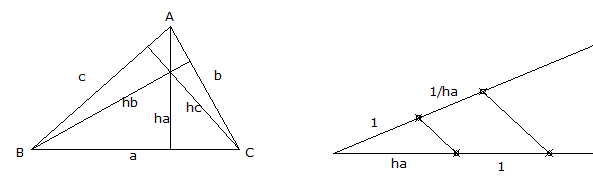En mi anterior comentario me limité a hallar la tercera altura, remitiendo a la solución final a cualquier construcción del triángulo a partir de sus alturas.
Siguiendo en la línea que inicié, adjunto una solución que he preparado de la misma forma.
"El área del triángulo formado por los inversos de las alturas es 1/4 de la inversa del área del triángulo original", siguiendo esta afirmación:
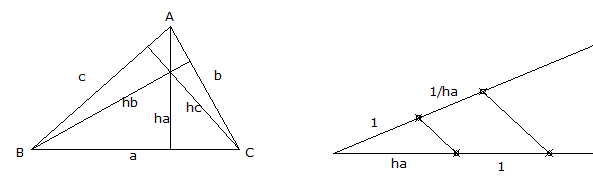
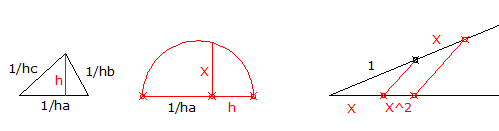
En la primera figura del gráfico un triángulo cualquiera del que conocemos sus alturas
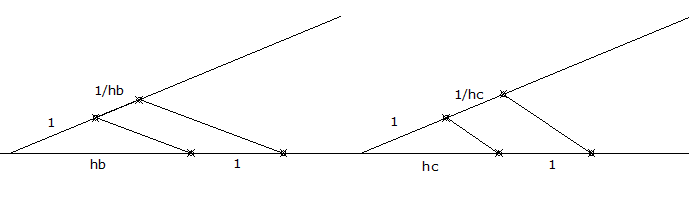
En la segunda, tercera y cuarta, por Tales construcción de los inversos de las alturas, partiendo de un segmento cualquiera auxiliar como unidad "1", que mantendremos a lo largo de la construcción
Quinta figura, triángulo formado con los segmentos inversos de las alturas, de rojo la altura "h" de este triángulo
En la sesta figura, por teorema de la altura, "X" raíz del doble del área de este triángulo
En la séptima, cuadrado de "X", doble del área de este triángulo
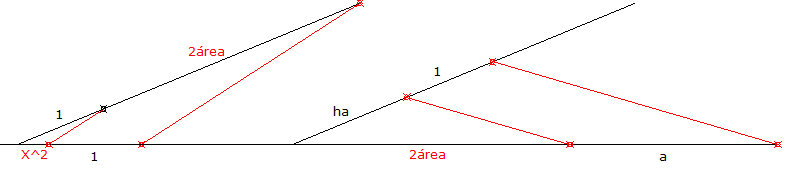
Octava, inversión de "X^2", resultando el doble del área del triángulo que se desea
Y en la novena construcción del lado "a"
Podríamos repetir este último paso para conseguir "b" y "c" o construir el triángulo dado un lado y alturas
Saludos
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí) El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado