no se hacer la parabola, me ayudan, gracias
puntos enlazados en una parábola *
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
puntos enlazados en una parábola *
Dados los puntos A, B y C enlazados en una parábola, una línea "a" paralela a su eje y una segunda línea r, encontrar la intersección de r con la parábola.
no se hacer la parabola, me ayudan, gracias
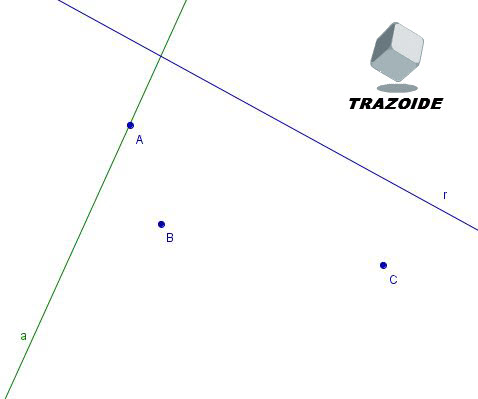
no se hacer la parabola, me ayudan, gracias
Hola.
De construcción de cónicas seguro que tienes aquí mismo o en Internet mucha información y además
con tanto friki experto en cónicas que hay por ahí, ni me debería atrever a contestar .
.
De todos modos, como me gusta "inventar" te adjunto una solución un tanto sui géneris.
Te recomiendo leer sobre la recta de Pascal, "alucinante" teorema de Pascal, muy útil en
el tema de las cónicas, sobre todo cuando se trata de obtener rectas tangentes o puntos de la misma.
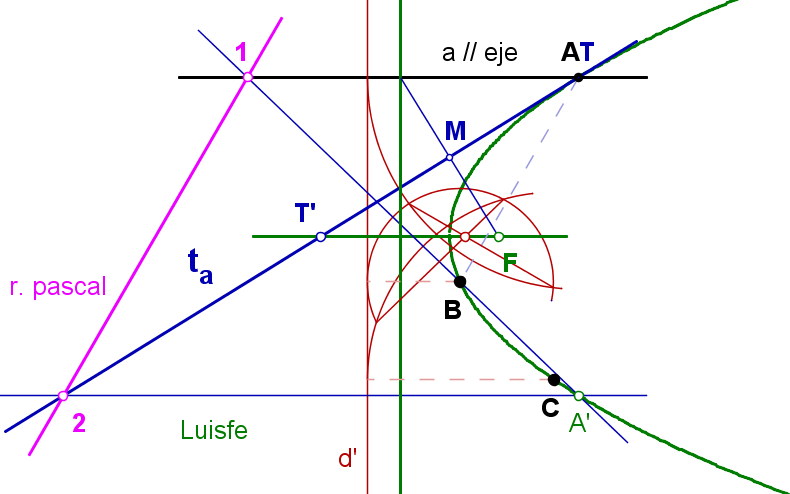
Comienzo trazando una perpendicular cualquiera (d') a la dirección del eje que será una directriz provisional.
Desde los puntos dados A,B,C trazo arcos tangentes a ella .
Las rectas de intersección entre los arcos se cruzan en un punto del eje.
Con el eje y dos puntos podemos obtener la parábola.
Halla el simétrico de A respecto al eje (A')
Paralela al eje `por A'
Recta A' B que corta en 1 a la recta "a" dada.
Paralela a AB por 1 que será la recta de Pascal que corta en 2 (paral por A')
Obtenemos una tangente "t_a" a la parábola uniendo 2 con A.
Esta corta al eje en T'.
La mediatriz AT' corta el eje en el ansiado foco F.
Ciao!
De construcción de cónicas seguro que tienes aquí mismo o en Internet mucha información y además
con tanto friki experto en cónicas que hay por ahí, ni me debería atrever a contestar
De todos modos, como me gusta "inventar" te adjunto una solución un tanto sui géneris.
Te recomiendo leer sobre la recta de Pascal, "alucinante" teorema de Pascal, muy útil en
el tema de las cónicas, sobre todo cuando se trata de obtener rectas tangentes o puntos de la misma.
Comienzo trazando una perpendicular cualquiera (d') a la dirección del eje que será una directriz provisional.
Desde los puntos dados A,B,C trazo arcos tangentes a ella .
Las rectas de intersección entre los arcos se cruzan en un punto del eje.
Con el eje y dos puntos podemos obtener la parábola.
Halla el simétrico de A respecto al eje (A')
Paralela al eje `por A'
Recta A' B que corta en 1 a la recta "a" dada.
Paralela a AB por 1 que será la recta de Pascal que corta en 2 (paral por A')
Obtenemos una tangente "t_a" a la parábola uniendo 2 con A.
Esta corta al eje en T'.
La mediatriz AT' corta el eje en el ansiado foco F.
Ciao!

¿Quién está conectado?
Usuarios navegando por este Foro: Google [Bot] y 11 invitados



