Un saludo y gracias.
triángulo con bisectriz interior y la bisectriz exterior *
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
triángulo con bisectriz interior y la bisectriz exterior *
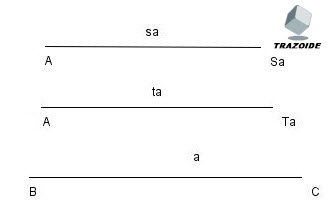
Dada la longitud del lado a = BC, ta la bisectriz interior del ángulo A y sa la bisectriz exterior del mismo ángulo, dibujar el triángulo ABC.
Un saludo y gracias.
Un saludo y gracias.
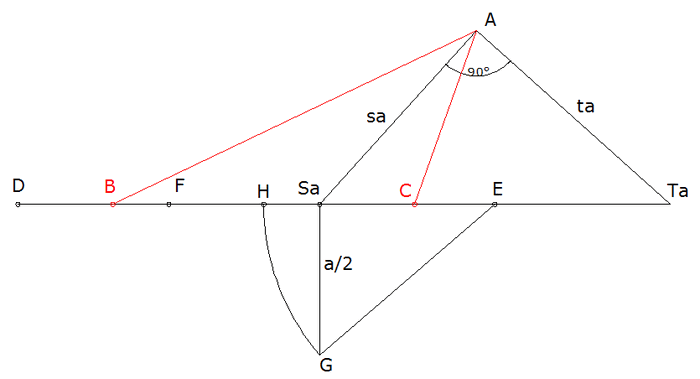
Construimos un triángulo rectángulo de catetos "sa" y "ta", la hipotenusa "TaSa" se solapará con la base "BC" del triángulo
A continuación de "Sa" colocamos un segmento "DSa" de valor "a" y otro perpendicular "GSa" de valor "a/2"
Por "E" punto medio de "TaSa" trazamos un arco de radio "EG" que corta a "DSa" en "H"
Si "F" es el punto medio de "DSa" "FH" es el segmento de solapamiento, si trasladamos "D" y "Sa" este valor, tenemos los vértices del triángulo deseado
Saludos
A continuación de "Sa" colocamos un segmento "DSa" de valor "a" y otro perpendicular "GSa" de valor "a/2"
Por "E" punto medio de "TaSa" trazamos un arco de radio "EG" que corta a "DSa" en "H"
Si "F" es el punto medio de "DSa" "FH" es el segmento de solapamiento, si trasladamos "D" y "Sa" este valor, tenemos los vértices del triángulo deseado
Saludos

triángulo lado , bisectrices interior y exterior del vértice opuesto
Hola, la verdad es que es un ejercicio muy interesante.
Si no os importa, voy a añadir unos apuntes un tanto improvisados y de paso muestro la misma solución que Seroig pero dándole la vuelta a la tortilla con el fin de darle un poco más de "perspectiva" al asunto.
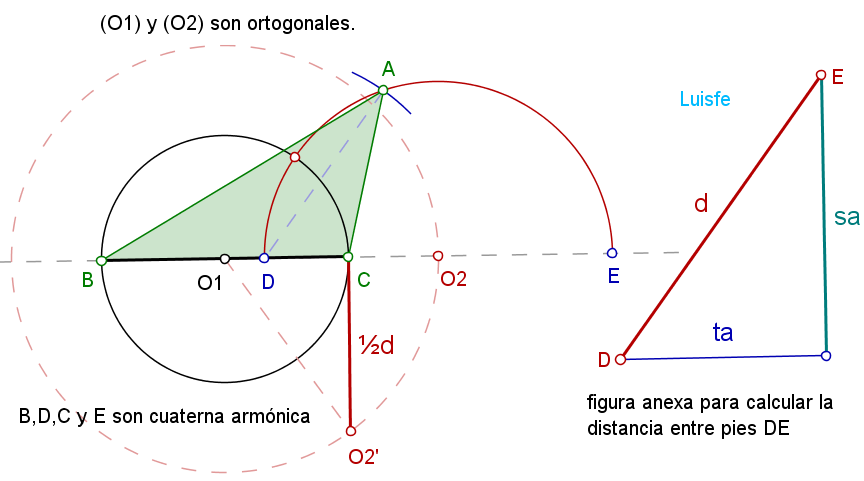
Los puntos diametrales en la misma recta de dos circunferencias ortogonales (O1) y (O2) forman una cuaterna armónica.
Los vértices B y C y los piés de las bisectrices D y E forman una cuaterna armónica.
Se trata de buscar entonces una circunferencia (O2) de diámetro DE o d ortogonal a (O1) (diámetro BC)
(O2) será el lugar geométrico de los vértices A cuyos pies de bisectrices (en BC y prolongación.) interiores y exteriores son constantes.
En la solución que muestro parto del lado BC en posición.
Para hallar el diámetro de la circunferencia ortogonal que queremos (O2)
Hallamos a parte un triángulo rectángulo de catetos ta y sa siendo la hipotenusa el diámetro d
Hallamos el lugar geométrico de los centros de las circunferencias ortogonales a (O1) de diámetro d obteniendo el centro (O2).
Dibujamos la semicircunferencia (O2) para obtener los pies de las bisectrices D y E.
Terminamos por hallar A sobre (O2) llevando la distancia de una de las dos bisectrices dadas.
Saludos.
Nota: Seroig ...te llamas Seroig, ¿recuerdas?
Si no os importa, voy a añadir unos apuntes un tanto improvisados y de paso muestro la misma solución que Seroig pero dándole la vuelta a la tortilla con el fin de darle un poco más de "perspectiva" al asunto.
Los puntos diametrales en la misma recta de dos circunferencias ortogonales (O1) y (O2) forman una cuaterna armónica.
Los vértices B y C y los piés de las bisectrices D y E forman una cuaterna armónica.
Se trata de buscar entonces una circunferencia (O2) de diámetro DE o d ortogonal a (O1) (diámetro BC)
(O2) será el lugar geométrico de los vértices A cuyos pies de bisectrices (en BC y prolongación.) interiores y exteriores son constantes.
En la solución que muestro parto del lado BC en posición.
Para hallar el diámetro de la circunferencia ortogonal que queremos (O2)
Hallamos a parte un triángulo rectángulo de catetos ta y sa siendo la hipotenusa el diámetro d
Hallamos el lugar geométrico de los centros de las circunferencias ortogonales a (O1) de diámetro d obteniendo el centro (O2).
Dibujamos la semicircunferencia (O2) para obtener los pies de las bisectrices D y E.
Terminamos por hallar A sobre (O2) llevando la distancia de una de las dos bisectrices dadas.
Saludos.

Nota: Seroig ...te llamas Seroig, ¿recuerdas?
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 40 invitados



