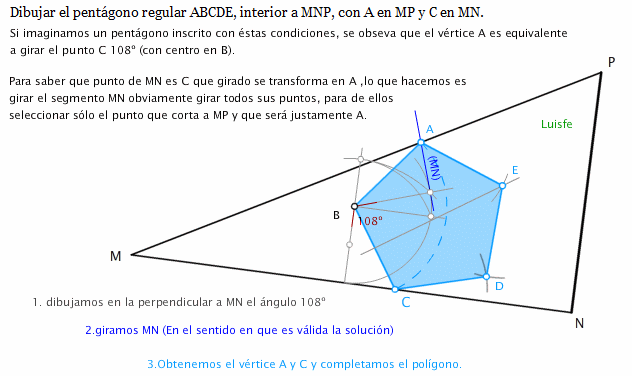
Es un tipo de giro especial, que utilizo cuando una de las ramas del ángulo que
quiero inscribir tiene distinta longitud.
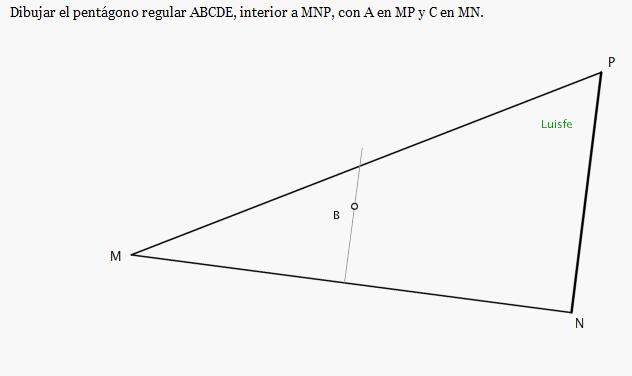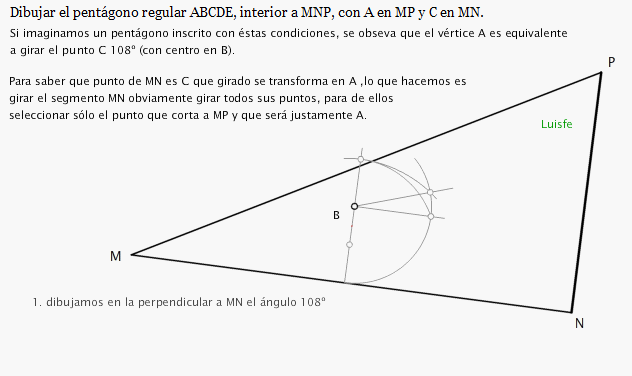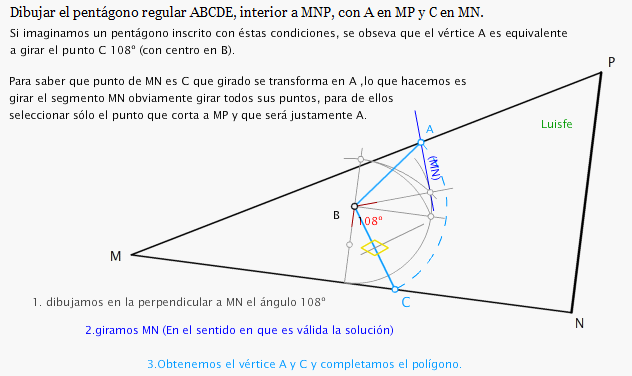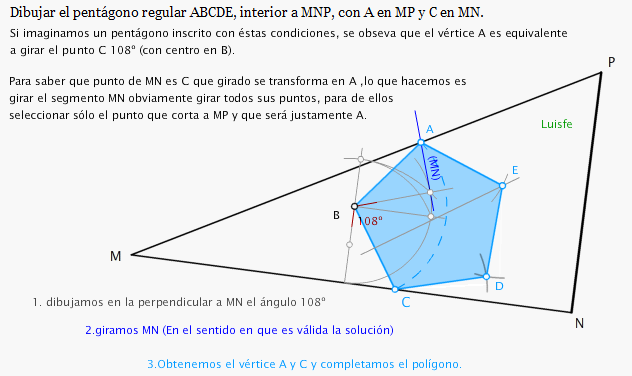
Mira ejemplos de giros clásicos en los que las figuras son regulares:
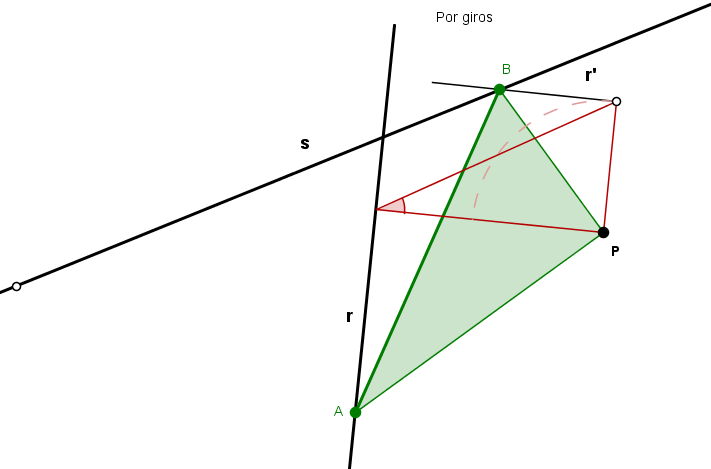
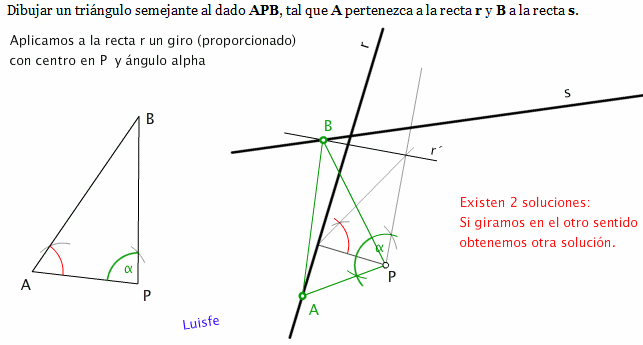
Ahora te pongo el ejemplo de un triángulo "feo" que queremos apoyar sobre
las rectas r y s. No tendremos la suerte de que el resultado tenga las mismas
medidas absolutas pero si semejante al dado por supuesto.
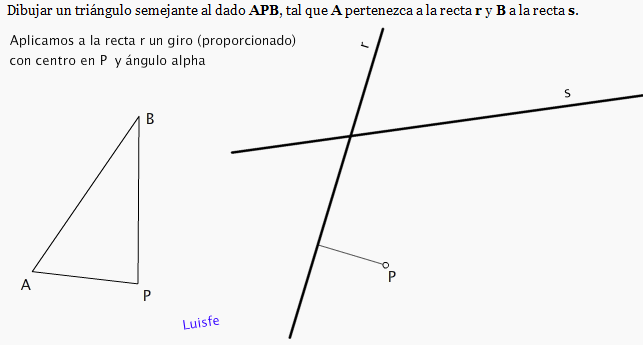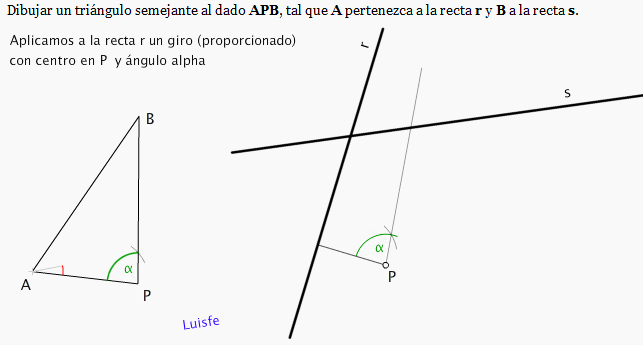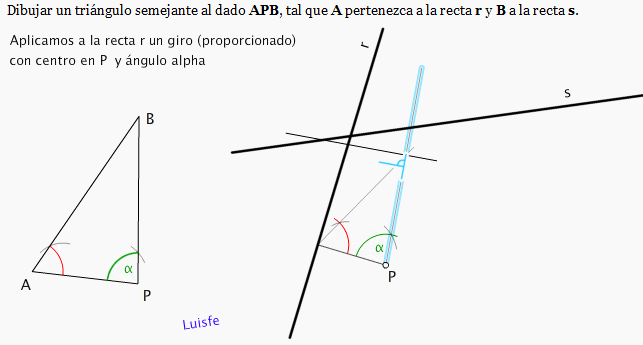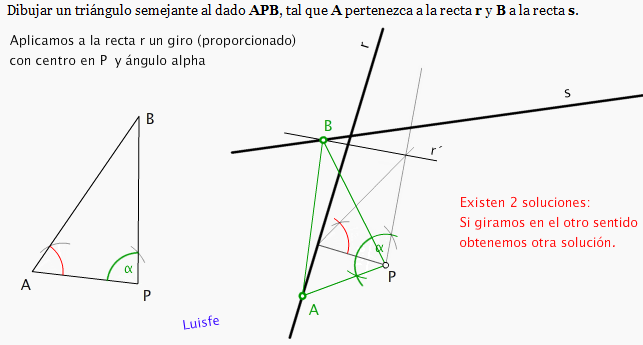
Lo que hago es proyectar una perpendicular (por comodidad) desde P a la recta r , su proyecciçon será A'.
con ésta peppendicular ,abro en P unl ángulo de giro = APB ., Para saber a qué distancia situo r' en el otro brazo (PB) abro en A'
otro ángulo PAB que me corta en B ' (ver dibujo) , en resumidas cuentas es dibujar un triángulo semejante con el lado PA perpendicular a r.
Ahora, la perpendicular a PB' por B' corta en la recta s en el punto B buscado, el resto es fácil.
És mucho más fácil hacerlo que explicarlo.
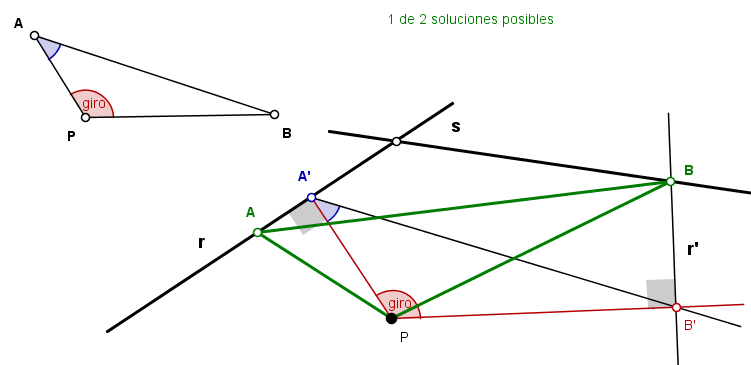
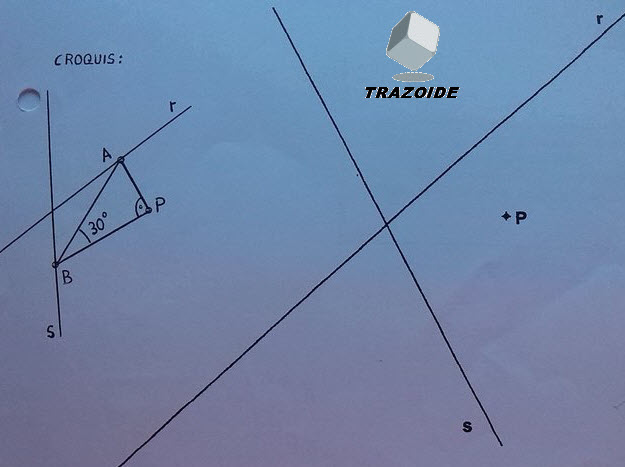
Añado una animación más:
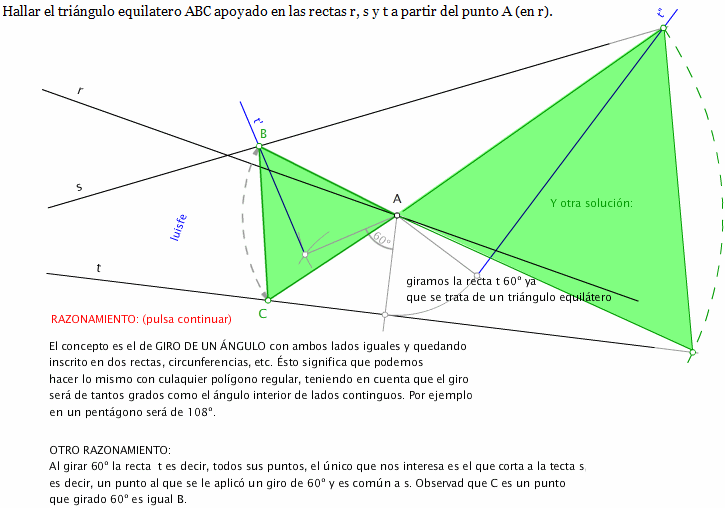
Imágenes fijas y en movimiento alternativas a las anteriores :
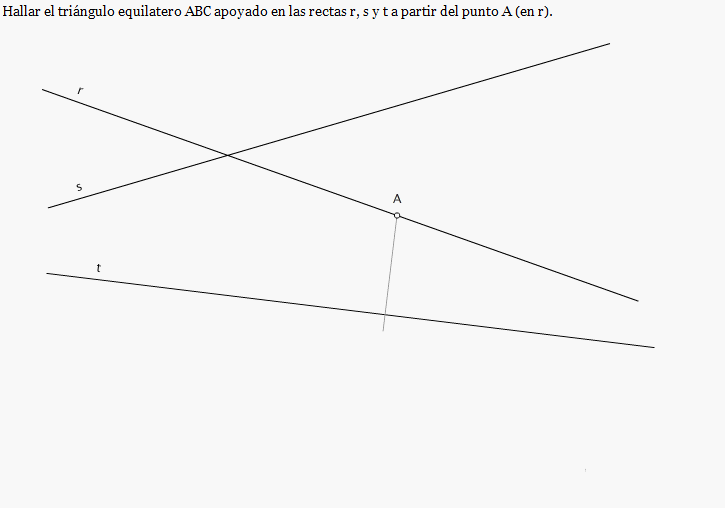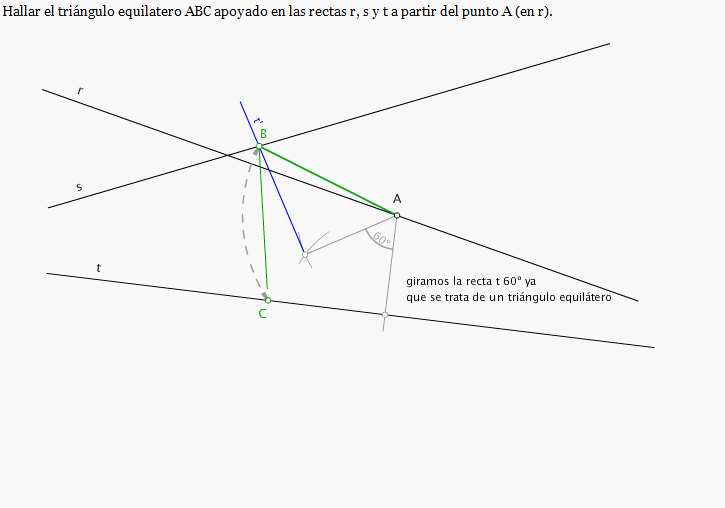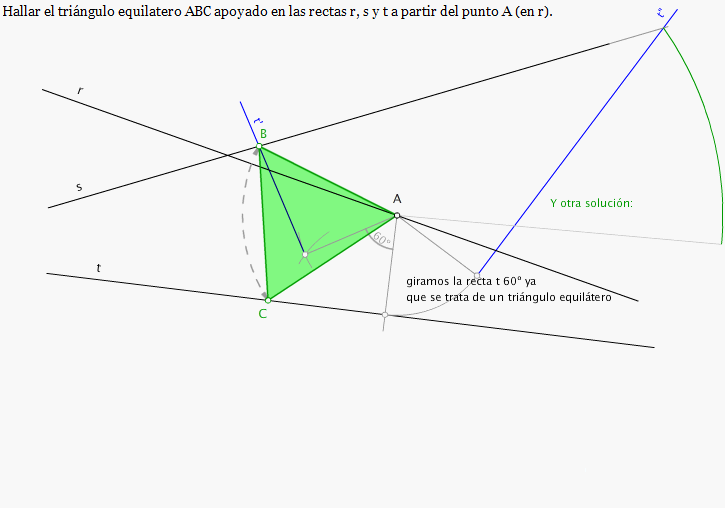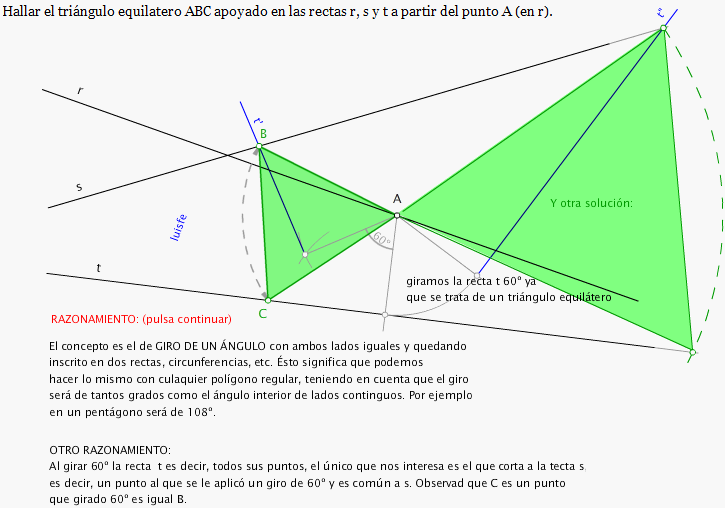

 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado